题目内容
15．${（{x^3}+\frac{1}{{\sqrt{x}}}）^n}$的展开式的所有二项式系数之和为128，则n为（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
分析 令x=1，可得2n=128，解得n．
解答 解：令x=1，可得2n=128，解得n=7．
故选：C．
点评 本题考查了二项式定理的性质及其应用，考查了推理能力与计算能力，属于基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
6．设$f（x）={x^3}+{log_2}（x+\sqrt{{x^2}+1}）$，则对任意实数a、b，若a+b≥0则（ ）
| A． | f（a）+f（b）≤0 | B． | f（a）+f（b）≥0 | C． | f（a）-f（b）≤0 | D． | f（a）-f（b）≥0 |
10．
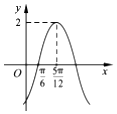函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）| A． | $f（x）=2sin（{x-\frac{π}{6}}）$ | B． | $f（x）=2sin（{2x-\frac{π}{3}}）$ | C． | $f（x）=2sin（{x+\frac{π}{12}}）$ | D． | $f（x）=2sin（{2x-\frac{π}{6}}）$ |
20．曲线$y=lnx-\frac{2}{x}$在x=1处的切线的倾斜角为α，则cosα+sinα的值为（ ）
| A． | $\frac{{2\sqrt{10}}}{5}$ | B． | $\frac{{\sqrt{10}}}{10}$ | C． | $\frac{{\sqrt{10}}}{5}$ | D． | $\frac{{3\sqrt{10}}}{10}$ |