题目内容
1.已知数列{an}是公差为2的等差数列,数列{bn}满足${b_1}=1,{b_2}=\frac{1}{2}$,若n∈N*时,anbn+1-bn+1=nbn.(Ⅰ)求{bn}的通项公式;
(Ⅱ)设${C_n}=\frac{1}{{{a_n}{a_{n+1}}}}$,求{Cn}的前n项和Sn.
分析 (Ⅰ)令n=1,可得a1=3,结合{an}是公差为2的等差数列,可得{an}的通项公式,将其代入已知条件anbn+1-bn+1=nbn来求{bn}的通项公式;
(Ⅱ)利用裂项相消法求和.
解答 解:(Ⅰ)∵anbn+1-bn+1=nbn.
当n=1时,a1b2-b2=b1.
∵${b_1}=1,{b_2}=\frac{1}{2}$,
∴a1=3,
又∵{an}是公差为2的等差数列,
∴an=2n+1,
则(2n+1)bn+1-bn+1=nbn.
化简,得
2bn+1=bn,即$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{1}{2}$,
所以数列{bn}是以1为首项,以$\frac{1}{2}$为公比的等比数列,
所以bn=($\frac{1}{2}$)n-1;
(Ⅱ)由(Ⅰ)知,an=2n+1,
所以${C_n}=\frac{1}{{{a_n}{a_{n+1}}}}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),
所以Sn=c1+c2+c3+…+cn
=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2n+1}$-$\frac{1}{2n+3}$)
=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{2n+3}$)
=$\frac{n}{6n+9}$.
点评 本题考查的知识点是数列的递推式,数列的通项公式,裂项相消法求和公式,难度中档.

练习册系列答案
相关题目
9.在区间[-1,3]内任取一个实数x满足log2(x-1)>0的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
16.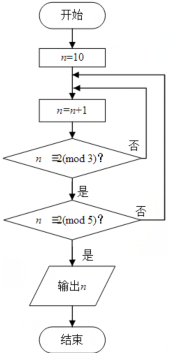 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
6.设$f(x)={x^3}+{log_2}(x+\sqrt{{x^2}+1})$,则对任意实数a、b,若a+b≥0则( )
| A. | f(a)+f(b)≤0 | B. | f(a)+f(b)≥0 | C. | f(a)-f(b)≤0 | D. | f(a)-f(b)≥0 |
10.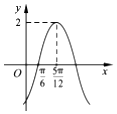 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )| A. | $f(x)=2sin({x-\frac{π}{6}})$ | B. | $f(x)=2sin({2x-\frac{π}{3}})$ | C. | $f(x)=2sin({x+\frac{π}{12}})$ | D. | $f(x)=2sin({2x-\frac{π}{6}})$ |