题目内容
18．已知双曲线$E：{x^2}-\frac{y^2}{3}=1$的左焦点为F，直线x=2与双曲线E相交于A，B两点，则△ABF的面积为（ ）| A． | 12 | B． | 24 | C． | $4\sqrt{3}$ | D． | $8\sqrt{3}$ |
分析 求出双曲线的左焦点，求出AB坐标，然后求解三角形的面积．
解答 解：双曲线$E：{x^2}-\frac{y^2}{3}=1$的左焦点为F（-2，0），
直线x=2与双曲线E相交于A，B两点，
则A（2，3），B（2，-3），
则△ABF的面积为：$\frac{1}{2}×$6×4=12．
故选：A．
点评 本题考查双曲线的简单性质的应用，考查计算能力．
练习册系列答案
相关题目
9．在区间[-1，3]内任取一个实数x满足log2（x-1）＞0的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
6．设$f（x）={x^3}+{log_2}（x+\sqrt{{x^2}+1}）$，则对任意实数a、b，若a+b≥0则（ ）
| A． | f（a）+f（b）≤0 | B． | f（a）+f（b）≥0 | C． | f（a）-f（b）≤0 | D． | f（a）-f（b）≥0 |
10．
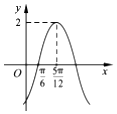函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）| A． | $f（x）=2sin（{x-\frac{π}{6}}）$ | B． | $f（x）=2sin（{2x-\frac{π}{3}}）$ | C． | $f（x）=2sin（{x+\frac{π}{12}}）$ | D． | $f（x）=2sin（{2x-\frac{π}{6}}）$ |