题目内容
16.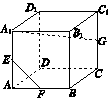 如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出EF与A1G所成的角.
解答 解: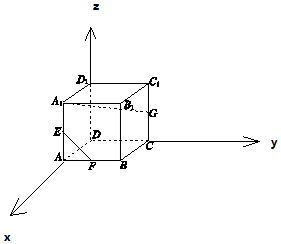 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,
则E(2,0,1),F(2,1,0),A1(2,0,2),G(0,2,1),
$\overrightarrow{EF}$=(0,1,-1),$\overrightarrow{{A}_{1}G}$=(-2,2,-1),
设EF与A1G所成的角为θ,
则cosθ=$\frac{|\overrightarrow{EF}•\overrightarrow{{A}_{1}G}|}{|\overrightarrow{EF}|•|\overrightarrow{{A}_{1}G}|}$=$\frac{3}{\sqrt{2}•3}$=$\frac{\sqrt{2}}{2}$,
∴θ=45°.
∴EF与A1G所成的角为45°.
故选:B.
点评 本题考查线线角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.设$f(x)={x^3}+{log_2}(x+\sqrt{{x^2}+1})$,则对任意实数a、b,若a+b≥0则( )
| A. | f(a)+f(b)≤0 | B. | f(a)+f(b)≥0 | C. | f(a)-f(b)≤0 | D. | f(a)-f(b)≥0 |
11.某班50人的一次竞赛成绩的频数分布如下:[60,70):3人,[70,80):16人,[80,90):24人,[90,100]:7人,利用各组区间中点值,可估计本次比赛该班的平均分为( )
| A. | 56 | B. | 68 | C. | 78 | D. | 82 |
6.设等差数列{an}的前n项和为Sn,且满足S2013>0,S2014<0,则前n项和Sn取最大值时n的值为( )
| A. | 1009 | B. | 1008 | C. | 1007 | D. | 1006 |