题目内容
已知sin(x-
)=-
,则sin2x= .
| π |
| 4 |
| 5 |
| 13 |
考点:二倍角的正弦
专题:三角函数的求值
分析:由已知可得sinx-cosx=-
,两边平方由二倍角的正弦公式可解得1-sin2x=
,从而得解.
5
| ||
| 13 |
| 50 |
| 169 |
解答:
解:∵sin(x-
)=-
,
∴
(sinx-cosx)=-
,解得:sinx-cosx=-
,
∴两边平方可得:1-sin2x=
,
∴解得:sin2x=
.
故答案为:
.
| π |
| 4 |
| 5 |
| 13 |
∴
| ||
| 2 |
| 5 |
| 13 |
5
| ||
| 13 |
∴两边平方可得:1-sin2x=
| 50 |
| 169 |
∴解得:sin2x=
| 119 |
| 169 |
故答案为:
| 119 |
| 169 |
点评:本题主要考查了二倍角的正弦公式的应用,两角差的正弦公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
f(x)=ex-x-2在下列那个区间必有零点( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
设复数eiθ=cosθ+isinθ,则复数e
i的虚部为( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
方程x2+y2+2x-4y-6=0表示的圆形是( )
A、以(1,-2)为圆心,
| ||
B、以(1,2)为圆心,
| ||
C、以(-1,-2)为圆心,
| ||
D、以(-1,2)为圆心,
|
正方体ABCD-A1B1C1D1中,AB1与C1D1所成的角( )
| A、30° | B、45° |
| C、60° | D、90° |
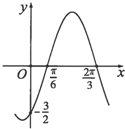 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<