题目内容
为了研究男羽毛球运动员的身高x（单位：cm）与体重y（单位：kg）的关系，通过随机抽样的方法，抽取5名运动员测得他们的身高与体重关系如下表：
①从这5个人中随机的抽取2个人，求这2个人体重之差的绝对值不小于2kg的概率；
②求回归直线方程
=bx+a．
| 身高（x） | 172 | 174 | 176 | 178 | 180 |
| 体重（y） | 74 | 73 | 76 | 75 | 77 |
②求回归直线方程
 |
| y |
考点：线性回归方程,古典概型及其概率计算公式
专题：计算题,概率与统计
分析：①列举出从这5个人中随机的抽取2个人，这2个人体重之差的绝对值不小于2kg的情况，即可求出概率；
②求出回归系数，即可求回归直线方程
=bx+a．
②求出回归系数，即可求回归直线方程
|
| y |
解答：
解：①抽取的2个人的体重为：
（74，73），（74，76），（74，75），（74，77）；
（73，76），（73，75），（73，77）；
（76，75），（76，77）；
（75，77）．
满足条件的有6种情况，…（4分）
故：2个人体重之差的绝对值不小于2kg的概率
=
． …（6分）
②
=
（172+174+176+178+180）=176，
=
（74+73+76+75+77）=75 …（8分）
b=
=0.4 …（11分）
∴a=75-0.4×176=4.6，
∴
=0.4x+4.6． …（12分）
（74，73），（74，76），（74，75），（74，77）；
（73，76），（73，75），（73，77）；
（76，75），（76，77）；
（75，77）．
满足条件的有6种情况，…（4分）
故：2个人体重之差的绝对值不小于2kg的概率
| 6 |
| 10 |
| 3 |
| 5 |
②
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
xi-
|
-4 | -2 | 0 | 2 | 4 | ||
yi-
|
-1 | -2 | 1 | 0 | 2 |
| 4+4+0+0+8 |
| 16+4+0+4+16 |
∴a=75-0.4×176=4.6，
∴
|
| y |
点评：本题考查概率的计算，考查回归直线方程，考查学生的计算能力，属于中档题．
练习册系列答案
特高级教师点拨系列答案
相关题目
设函数f1（x）=x2，f2（x）=2（x-x2），f3(x)=
|sin2πx|，ai=
，i=0，1，2，…，99．记Ik=|fk（a1）-fk（a0）|+|fk（a2）-fk（a1）丨+…+|fk（a99）-fk（a98）|，k=1，2，3，则（ ）
| 1 |
| 3 |
| i |
| 99 |
| A、I1＜I2＜I3 |
| B、I2＜I1＜I3 |
| C、I1＜I3＜I2 |
| D、I3＜I2＜I1 |
在如图所示的空间直角坐标系O-xyz中，一个四面体的顶点坐标分别为（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出的编号为①，②，③，④的四个图，则该四面体的正视图和俯视图分别为（ ）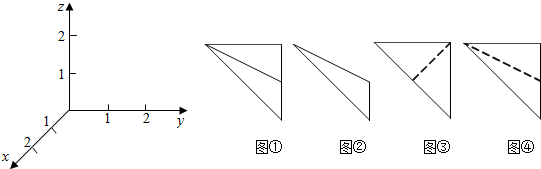
| A、①和② | B、③和① |
| C、④和③ | D、④和② |
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-3x，则函数g（x）=f（x）-x+3的零点的集合为（ ）
| A、{1，3} | ||
| B、{-3，-1，1，3} | ||
C、{2-
| ||
D、{-2-
|
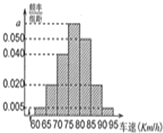2014年“五一节”期间，高速公路车辆较多，交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度，采用的方法是：按到达监控点先后顺序，每隔50辆抽取一辆，总共抽取120辆，分别记下其行车速度，将行车速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如图所示的频率分布直方图，据图解答下列问题：