题目内容
在如图所示的空间直角坐标系O-xyz中，一个四面体的顶点坐标分别为（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出的编号为①，②，③，④的四个图，则该四面体的正视图和俯视图分别为（ ）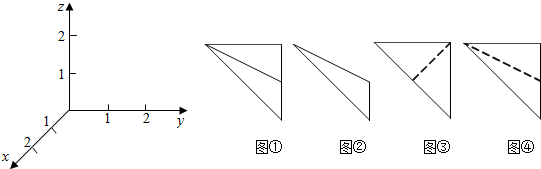
| A、①和② | B、③和① |
| C、④和③ | D、④和② |
考点：简单空间图形的三视图
专题：计算题,空间位置关系与距离
分析：在坐标系中，标出已知的四个点，根据三视图的画图规则，可得结论．
解答：
解：在坐标系中，标出已知的四个点，根据三视图的画图规则，可得三棱锥的正视图和俯视图分别为④②，
故选：D．
解：在坐标系中，标出已知的四个点，根据三视图的画图规则，可得三棱锥的正视图和俯视图分别为④②，故选：D．
点评：本题考查三视图的画法，做到心中有图形，考查空间想象能力，是基础题．
练习册系列答案
相关题目
已知F为双曲线C：x2-my2=3m（m＞0）的一个焦点，则点F到C的一条渐近线的距离为（ ）
A、
| ||
| B、3 | ||
C、
| ||
| D、3m |
已知全集U={1，2，3，4，5，6，7}，集合A={1，3，5，6}，则∁UA=（ ）
| A、{1，3，5，6} |
| B、{2，3，7} |
| C、{2，4，7} |
| D、{2，5，7} |
下列叙述中正确的是（ ）
| A、若a，b，c∈R，则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” |
| B、若a，b，c∈R，则“ab2＞cb2”的充要条件是“a＞c” |
| C、命题“对任意x∈R，有x2≥0”的否定是“存在x∈R，有x2≥0” |
| D、l是一条直线，α，β是两个不同的平面，若l⊥α，l⊥β，则α∥β |
在等差数列{an}中，a1=2，a3+a5=10，则a7=（ ）
| A、5 | B、8 | C、10 | D、14 |
