题目内容
对任意复数ω1，ω2，定义ω1*ω2=ω1
2，其中
2是ω2的共轭复数，对任意复数z1，z2，z3有如下命题：
①（z1+z2）*z3=（z1*z3）+（z2*z3）
②z1*（z2+z3）=（z1*z2）+（z1*z3）
③（z1*z2）*z3=z1*（z2*z3）；
④z1*z2=z2*z1
则真命题的个数是（ ）
. |
| ω |
. |
| ω |
①（z1+z2）*z3=（z1*z3）+（z2*z3）
②z1*（z2+z3）=（z1*z2）+（z1*z3）
③（z1*z2）*z3=z1*（z2*z3）；
④z1*z2=z2*z1
则真命题的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：命题的真假判断与应用,复数代数形式的乘除运算
专题：简易逻辑,数系的扩充和复数
分析：根据已知中ω1*ω2=ω1
2，其中
2是ω2的共轭复数，结合复数的运算性质逐一判断四个结论的真假，可得答案．
. |
| ω |
. |
| ω |
解答：
解：①（z1+z2）*z3=（z1+z2）
=（z1
+z2
=（z1*z3）+（z2*z3），正确；
②z1*（z2+z3）=z1（
）=z1（
+
）=z1
+z1
=（z1*z2）+（z1*z3），正确；
③（z1*z2）*z3=z1
，z1*（z2*z3）=z1*（z2
）=z1（
）=z1
z3，等式不成立，故错误；
④z1*z2=z1
，z2*z1=z2
，等式不成立，故错误；
综上所述，真命题的个数是2个，
故选：B
. |
| z3 |
. |
| z3 |
. |
| z3 |
②z1*（z2+z3）=z1（
. |
| z2+z3 |
| z2 |
. |
| z3 |
| z2 |
. |
| z3 |
③（z1*z2）*z3=z1
| z2 |
. |
| z3 |
. |
| z3 |
. | ||
z2
|
| z2 |
④z1*z2=z1
| z2 |
. |
| z1 |
综上所述，真命题的个数是2个，
故选：B
点评：本题以命题的真假判断为载体，考查了复数的运算性质，细心运算即可，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
若变量x，y满足约束条件
，则2x+y的最大值是（ ）
|
| A、2 | B、4 | C、7 | D、8 |
下列叙述中正确的是（ ）
| A、若a，b，c∈R，则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” |
| B、若a，b，c∈R，则“ab2＞cb2”的充要条件是“a＞c” |
| C、命题“对任意x∈R，有x2≥0”的否定是“存在x∈R，有x2≥0” |
| D、l是一条直线，α，β是两个不同的平面，若l⊥α，l⊥β，则α∥β |
设F1，F2分别为双曲线
-
=1（a＞0，b＞0）的左、右焦点，双曲线上存在一点P使得（|PF1|-|PF2|）2=b2-3ab，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、4 | ||
D、
|
随机掷两枚质地均匀的骰子，它们向上的点数之和不超过5的概率记为p1，点数之和大于5的概率记为p2，点数之和为偶数的概率记为p3，则（ ）
| A、p1＜p2＜p3 |
| B、p2＜p1＜p3 |
| C、p1＜p3＜p2 |
| D、p3＜p1＜p2 |
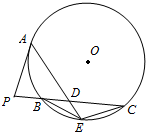如图，P是⊙O外一点，PA是切线，A为切点，割线PBC与⊙O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交⊙O于点E，证明：