题目内容
2.抛物线2y2+x=0的焦点坐标是:(-$\frac{1}{8}$,0),准线方程是:x=$\frac{1}{8}$.分析 将抛物线化成标准方程得y2=-$\frac{1}{2}$x,根据抛物线的基本概念即可算出该抛物线的焦点坐标、准线方程.
解答 解:∵抛物线的方程为2y2+x=0,
∴化成标准方程,得y2=-$\frac{1}{2}$x,
由此可得抛物线的2p=$\frac{1}{2}$,得$\frac{p}{2}$=$\frac{1}{8}$
∴抛物线的焦点坐标为(-$\frac{1}{8}$,0),准线方程是x=$\frac{1}{8}$,
故答案为(-$\frac{1}{8}$,0),x=$\frac{1}{8}$.
点评 本题给出抛物线的方程,求抛物线的焦点坐标、准线方程,着重考查了抛物线的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.集合M={(x,y)|x2+y2=1},N={(x,y)|x2+y2=4},集合M与N的关系是( )
| A. | M=N | B. | M⊆N | ||
| C. | N⊆M | D. | M,N不存在包含关系 |
14.抛物线x=2ay2的准线方程是x=2,则a的值是( )
| A. | $\frac{1}{16}$ | B. | $-\frac{1}{16}$ | C. | -4 | D. | 4 |
11.已知抛物线x=4y2上一点P(m,1),焦点为F.则|PF|=( )
| A. | m+1 | B. | 2 | C. | $\frac{63}{16}$ | D. | $\frac{65}{16}$ |
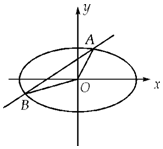 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列,记△AOB的面积为S.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列,记△AOB的面积为S.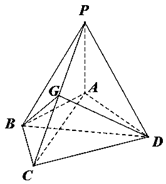 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,∠ABC=120°,G为线段PC上的点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,∠ABC=120°,G为线段PC上的点.