题目内容
推理“①正方形是平行四边形；②梯形不是平行四边形；③所以梯形不是正方形”中的小前提是（ ）
| A、① | B、② | C、③ | D、①和② |
考点：演绎推理的基本方法
专题：推理和证明
分析：根据所给的条件可与得到这样一个结论：正方形是平行四边形，梯形不是平行四边形，所以梯形不是正方形，得到小前提是梯形不是平行四边形，
解答：
解：根据所给的三个条件①正方形是平行四边形
②梯形不是平行四边形
③所以梯形不是正方形，
可与得到这样一个结论：正方形是平行四边形，梯形不是平行四边形，所以梯形不是正方形，
∴小前提是梯形不是平行四边形，
故选：B
②梯形不是平行四边形
③所以梯形不是正方形，
可与得到这样一个结论：正方形是平行四边形，梯形不是平行四边形，所以梯形不是正方形，
∴小前提是梯形不是平行四边形，
故选：B
点评：本题考查三段论形式的推导过程，在这种推导过程中，三部分都可以作为考查的对象出现，本题是一个基础题，若出现一定是一个送分题目
练习册系列答案
阅读快车系列答案
相关题目
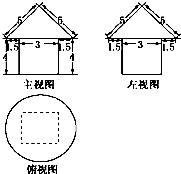如图是一建筑物的三视图及其尺寸（单位：m），建筑师要在此建筑物的外壁用油漆刷一遍，若每平方米需用油漆0.2kg，则共用的油漆为（ ）（π取3.14，结果精确到0.01kg）| A、22.87 kg |
| B、24.67 kg |
| C、26.47 kg |
| D、28.27 kg |
已知角α的终边上一点的坐标为（sin
，cos
），则角α的最小正值为（ ）
| π |
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|