题目内容
计算2sin14°•cos31°+sin17°等于（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点：两角和与差的正弦函数
专题：计算题,三角函数的求值
分析：将17°=31°-14°，运用两角差的正弦公式，化简再运用两角和的正弦公式，注意逆用公式．
解答：
解：2sin14°•cos31°+sin17°
=2sin14°•cos31°+sin（31°-14°）
=2sin14°cos31°+sin31°cos14°-cos31°sin14°
=sin31°cos14°+cos31°sin14°
=sin（31°+14°）=sin45°=
．
故选A．
=2sin14°•cos31°+sin（31°-14°）
=2sin14°cos31°+sin31°cos14°-cos31°sin14°
=sin31°cos14°+cos31°sin14°
=sin（31°+14°）=sin45°=
| ||
| 2 |
故选A．
点评：本题考查三角函数值的求法，考查两角和差的正弦公式的运用，属于中档题．
练习册系列答案
相关题目
有穷数列1，23，26，29，…，23n+6的项数是（ ）
| A、3n+7 | B、3n+6 |
| C、n+3 | D、n+2 |
已知A（-2，0），B（0，2），实数k是常数，M，N是圆x2+y2+kx=0上两个不同点，且M，N关于直线x-y-1=0对称，若P是圆x2+y2+kx=0上的动点，则△PAB面积的最大值是（ ）
A、3-
| ||
| B、4 | ||
C、3+
| ||
| D、6 |
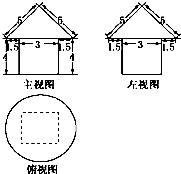如图是一建筑物的三视图及其尺寸（单位：m），建筑师要在此建筑物的外壁用油漆刷一遍，若每平方米需用油漆0.2kg，则共用的油漆为（ ）（π取3.14，结果精确到0.01kg）| A、22.87 kg |
| B、24.67 kg |
| C、26.47 kg |
| D、28.27 kg |