题目内容
已知直线l经过点(2,
),其横截距与纵截距分别为a,b(a,b均为正数),则使a+b≥c恒成立的c的取值范围( )
| 1 |
| 2 |
A、(-∞,
| ||
| B、(0,1] | ||
| C、(-∞,9) | ||
| D、(-∞,8] |
考点:恒过定点的直线
专题:计算题,直线与圆
分析:由已知设出直线l的截距式方程,代入已知点的坐标得到
+
=1,然后灵活运用“1”的代换借助于基本不等式求a+b的最小值,则使a+b≥c恒成立的c的取值范围为可求.
| 2 |
| a |
| 1 |
| 2b |
解答:
解:∵直线l的横截距与纵截距分别为a、b(a、b均为正数),且直线l经过点(2,
),
∴可设直线l的方程为
+
=1,则
+
=1.
∵a+b=(a+b)(
+
)=
+2+
+
≥
(当且仅当
=
时取等号).
则使a+b≥c恒成立的c的取值范围为(-∞,
].
故选:A.
| 1 |
| 2 |
∴可设直线l的方程为
| x |
| a |
| y |
| b |
| 2 |
| a |
| 1 |
| 2b |
∵a+b=(a+b)(
| 2 |
| a |
| 1 |
| 2b |
| 1 |
| 2 |
| 2b |
| a |
| a |
| 2b |
| 9 |
| 2 |
| 2b |
| a |
| a |
| 2b |
则使a+b≥c恒成立的c的取值范围为(-∞,
| 9 |
| 2 |
故选:A.
点评:本题考查恒成立问题,考查了直线的截距式方程,训练了利用基本不等式求最值,解答此题的关键是对“1”的灵活运用,是中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
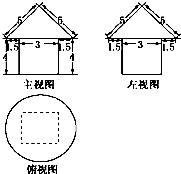 如图是一建筑物的三视图及其尺寸(单位:m),建筑师要在此建筑物的外壁用油漆刷一遍,若每平方米需用油漆0.2kg,则共用的油漆为( )(π取3.14,结果精确到0.01kg)
如图是一建筑物的三视图及其尺寸(单位:m),建筑师要在此建筑物的外壁用油漆刷一遍,若每平方米需用油漆0.2kg,则共用的油漆为( )(π取3.14,结果精确到0.01kg)| A、22.87 kg |
| B、24.67 kg |
| C、26.47 kg |
| D、28.27 kg |
已知角α的终边上一点的坐标为(sin
,cos
),则角α的最小正值为( )
| π |
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
直线l1:2x+y+1=0与l2:3x+4y-1=0的交点坐标为( )
| A、(1,-3) |
| B、(-2,1) |
| C、(-5,4) |
| D、(-1,1) |
