题目内容
15.已知定义在(0,+∞)的函数f(x),其导函数为f′(x),满足:f(x)>0且$\frac{2x+3}{x}>-\frac{{{f^'}(x)}}{f(x)}$总成立,则下列不等式成立的是( )| A. | e2e+3f(e)<e2ππ3f(π) | B. | e2e+3f(π)>e2ππ3f(e) | C. | e2e+3f(π)<e2ππ3f(e) | D. | e2e+3f(e)>e2ππ3f(π) |
分析 令g(x)=e2xx3f(x),g′(x)=)=e2xx2[(2x+3)f(x)+xf′(x)]>0,⇒g(x)=e2xx3f(x)在(0,+∞)上单调递增⇒g(e)<g(π),即可得到.
解答 解:∵f(x)>0且$\frac{2x+3}{x}>-\frac{{{f^'}(x)}}{f(x)}$总成立,∴(2x+3)f(x)+xf′(x)>0.
令g(x)=e2xx3f(x),g′(x)=)=e2xx2[(2x+3)f(x)+xf′(x)]>0,
∴g(x)=e2xx3f(x)在(0,+∞)上单调递增,∴g(e)<g(π),
∴e2e+3f(e)<e2ππ3f(π),故选:A.
点评 本题考查了构造新函数,处理不等式问题,属于压轴题.

练习册系列答案
相关题目
3.运行下面的程序中,若输入x的值为5,则输出的y的值为( )


| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
7.周长为9,圆心角为1rad的扇形面积为( )
| A. | $\frac{9}{2}$ | B. | $\frac{9}{4}$ | C. | π | D. | 2 |




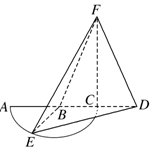 如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.
如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.