题目内容
10.已知函数$f(x)=\left\{\begin{array}{l}{x^2}+2x,(x≥0)\\-{x^2}+2x,(x<0)\end{array}\right.$,若f(a)+f(a2-2)<0,则实数a的取值范围是( )| A. | (-∞,-1)∪(2,+∞) | B. | (-1,2) | C. | (-2,1) | D. | (-∞,-2)∪(1,+∞) |
分析 根据分段函数的表达式,结合函数奇偶性和单调性的定义先判断函数的单调性和奇偶性,然后将不等式进行转化求解即可得到结论.
解答  解:若x<0,则-x>0,此时f(-x)=x2-2x=-(-x2+2x)=-f(x),
解:若x<0,则-x>0,此时f(-x)=x2-2x=-(-x2+2x)=-f(x),
若x>0,则-x<0,此时f(-x)=-x2-2x=-(x2+2x)=-f(x),
∵f(0)=0,∴恒有f(-x)=-f(x),即函数f(x)是奇函数,
当x≥0时,y=x2+2x=(x+1)2-1递增,
当x<0时,y=2x-x2=-(x-1)2+1递增,且f(0)=0,
则f(x)在定义域R上是增函数,
则f(a)+f(a2-2)<0等价为f(a2-2)<-f(a)=f(-a),
即:a2-2<-a,即a2+a-2<0,
解得:-2<a<1
∴实数a的取值范围是(-2,1),
故选:C.
点评 本题主要考查函数不等式的求解,利用分段函数的性质判断函数的单调性和奇偶性是解决本题的关键.一般来讲,抽象函数不等式,多数用单调性定义或数形结合法求解.

练习册系列答案
相关题目
18.已知△ABC的三条边长为a,b,c,则“△ABC是等边三角形”是“a2+b2+c2=ab+ac+bc”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,且它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点,则椭圆C的标准方程为( )
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 |
15.已知函数f(x)=2${\;}^{{{({a-x})}^k}}}$(a∈R),且f(1)>f(3),f(2)>f(3)( )
| A. | 若k=1,则|a-1|<|a-2| | B. | 若k=1,则|a-1|>|a-2| | C. | 若k=2,则|a-1|<|a-2| | D. | 若k=2,则|a-1|>|a-2| |
2.(x2-$\frac{3}{{x}^{3}}$)5的展开式中常数项为( )
| A. | 270 | B. | -270 | C. | -90 | D. | 90 |
19.已知向量$\overrightarrow{a}$=($\frac{1}{2}$,k),$\overrightarrow{b}$=(k-1,4),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数k的值为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | -$\frac{1}{7}$ | D. | 2 |
20.李华经营了两家电动轿车销售连锁店,其月利润(单位:元)分别为L1=-5x2+900x-10000,L2=300x-1000(其中x为销售辆数),若某月两连锁店共销售了110辆,则能获得的最大利润为( )
| A. | 11000 | B. | 22000 | C. | 33000 | D. | 40000 |
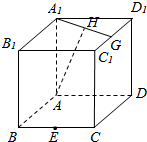 如图,棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D&1的中点,H为A1G的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D&1的中点,H为A1G的中点.