题目内容

2．（x2-$\frac{3}{{x}^{3}}$）5的展开式中常数项为（　　）
A．270B．-270C．-90D．90

分析 在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得展开式的常数项．

解答 解：（x2-$\frac{3}{{x}^{3}}$）5的展开式的通项公式为Tr+1=${C}_{5}^{r}$•（-3）r•x10-5r，
令10-5r=0，求得r=2，可得展开式中常数项为${C}_{5}^{2}$•9=90，
故选：D．

点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于基础题．

练习册系列答案
相关题目
10．A、B是抛物线y2=2px（p＞0）上的两点，满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0（O是原点），求证：
（1）A、B两点的横坐标之积，纵坐标之积均为定值．
（2）直线AB过定点．
13．已知a，b是实数，函数f（x）=x|x-a|+b．
（1）当a=2时，求函数f（x）的单调区间；
（2）若存在a∈[-3，5]，使得函数f（x）在[-4，5]上恒有三个零点，求b的取值范围．
10．已知函数$f（x）=\left\{\begin{array}{l}{x^2}+2x，（x≥0）\\-{x^2}+2x，（x＜0）\end{array}\right.$，若f（a）+f（a2-2）＜0，则实数a的取值范围是（　　）
A．（-∞，-1）∪（2，+∞）B．（-1，2）C．（-2，1）D．（-∞，-2）∪（1，+∞）
17．在△ABC中，内角A，B，C所对的边分别是a，b，c．已知acosB=bcosA，边BC上的中线长为4．
（Ⅰ）若$A=\frac{π}{6}$，求c；
（Ⅱ）求△ABC面积的最大值．
7．设函数f（x）=lg（x2-2x-3）的定义域为集合A，函数$g（x）=\sqrt{2-|x|}$的定义域为集合B，定义集合A-B={x|x∈A且x∉B}．
（1）求A-B；
（2）若C={x|m-1＜x＜2m+1}，C⊆B，求实数m的取值范围．
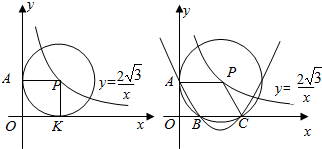14．在直角坐标系xOy中，已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$（x＞0）图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．
（1）如图1，⊙P运动到与x轴相切，设切点为K，判断四边形OKPA的形状，并说明理由．
（2）如图2，⊙P运动到与x轴相交，设交点为B，C．当四边形ABCP是菱形时：
①求出点A，B，C的坐标．
②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的$\frac{1}{2}$？若存在，试求出所有满足条件的M点的坐标；若不存在，试说明理由．
11．已知集合A={x|2x＞1}，B={ x|x＜1}，则A∩B?（　　）
A．{ x|0＜x＜1}B．{ x|x＞?0}C．{ x|x＞1}D．{x|x＜1}
12．在平面直角坐标系xoy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C1的极坐标方程为pcos（θ-$\frac{π}{3}$）=-1，曲线C2的参数方程为$\left\{\begin{array}{l}{x=1+\sqrt{2}cosα}\\{y=1+\sqrt{2}sinα}\end{array}\right.$，（其中α为参数，α∈[0，2π）），点A，B分别在曲线C1，C2上．
（1）求曲线C1的直角坐标方程和曲线C2的普通方程；
（2）试求两曲线上点A，B距离的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网