题目内容
12.已知函数f(x)=ex+$\frac{ax}{x+1}$-1(a∈R且a为常数).(1)当a=-1时,讨论函数f(x)在(-1,+∞)的单调性;
(2)设y=t(x)可求导数,且它的导函数t′(x)仍可求导数,则t′(x)再次求导所得函数称为原函数y=t(x)的二阶函数,记为t′′(x),利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间[a,b]上是凸函数的充要条件是这个函数在(a,b)的二阶导函数非负.
若g(x)=(x+1)[f(x)+1]+(a-$\frac{1}{{2}^{{e}^{4}}}$)x2在(-∞,-1)不是凸函数,求a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出函数g(x)的二阶导数,问题转化为a≥$\frac{1}{{2e}^{4}}$-$\frac{1}{2}$(x+3)ex,令h(x)=$\frac{1}{{2e}^{4}}$-$\frac{1}{2}$(x+3)ex,根据函数的单调性求出a的范围即可.
解答 解:(1)f′(x)=ex-$\frac{1}{{(x+1)}^{2}}$,
令f′(x)=0,解得:x=0,
设r(x)=ex-$\frac{1}{{(x+1)}^{2}}$,则r′(x)=ex+$\frac{2}{{(x+1)}^{3}}$,
当x>-1时,r′(x)>0,r(x)在(-1,+∞)上是单调增函数,
故x=0是r(x)在(-1,+∞)内的唯一零点,
即x=0是f′(x)在(-1,+∞)内的唯一零点,
所以当-1<x<0时,f′(x)<0,即f(x)在(-1,0)上是单调减函数;
当x>0时,f′(x)>0,即f(x)在(0,+∞)上是单调增函数.
(II)g(x)=(x+1)[f(x)+1]+(a-$\frac{1}{{2e}^{4}}$)x2=(x+1)ex+(a-$\frac{1}{{2e}^{4}}$)x2+ax,
g′(x)=(x+2)ex+2(a-$\frac{1}{{2e}^{4}}$)x+a,g″(x)=(x+3)ex+2(a-$\frac{1}{{2e}^{4}}$),
如果g(x)在(-∞,-1)是凸函数,那么?x∈(-∞,-1)都有g″(x)≥0,
g″(x)≥0⇒a≥$\frac{1}{{2e}^{4}}$-$\frac{1}{2}$(x+3)ex,
令h(x)=$\frac{1}{{2e}^{4}}$-$\frac{1}{2}$(x+3)ex,即得h′(x)=-$\frac{1}{2}$(x+4)ex,
h′(x)=0⇒x=-4,当x<-4时,h′(x)>0,当-4<x<-1时,h′(x)<0,
即h(x)在(-∞,-4)单调递增,在(-4,-1)单调递减,所以h(x)≤h(-4)=e-4,
即a≥e-4,又g(x)在(-∞,-1)不是凸函数,
所以a∈(-∞,e-4).
点评 本题考查了函数的单调性、函数恒成立问题,考查导数的应用以及转化思想,是一道中档题.

 名校课堂系列答案
名校课堂系列答案| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 3 | 3 | 3 | 1 |
(Ⅰ)求理科组恰好记4分的概率;
(Ⅱ)设文科组男生被选出的人数为X,求随机变量的分布列X和数学期望E(x).
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2$\sqrt{2}$ | D. | 2 |
 如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )| A. |  | B. |  | C. | 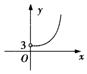 | D. |  |
| A. | i(1-i)2 | B. | i2(1+i) | C. | (1-i)2 | D. | i(1+i) |