题目内容
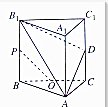 如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:
如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:(1)平面AB1D⊥平面ABB1A1;
(2)OP∥平面AB1D.
考点:直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)要证平面AB1D⊥平面ABB1A1;只要证A1B⊥平面ADB1,根据直线与平面垂直的判定定理可知,只需证A1B与平面ADB1内两相交直线垂直,而AB1⊥A1B,AB1⊥DO,A1B∩DO=O,满足定理所需条件.
(2)连接CO并延长交AB于Q,则Q为AB的中点,连接CP,PQ,证明PC∥B1D,PQ∥B1A,利用面面平行的判定定理,可得平面PQC∥平面AB1D,即可证明OP∥平面AB1D.
(2)连接CO并延长交AB于Q,则Q为AB的中点,连接CP,PQ,证明PC∥B1D,PQ∥B1A,利用面面平行的判定定理,可得平面PQC∥平面AB1D,即可证明OP∥平面AB1D.
解答:
证明:(1)连A1B,与AB1相交于E,连接DE,过C作CF⊥AB,则F为BC中点,
∵ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,
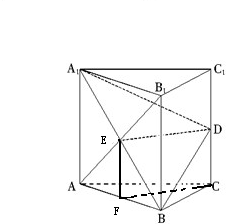
∴Rt△ACD≌Rt△B1C1D,∴AD=B1D
又E是AB1的中点,∴AB1⊥DE,DE∥CF,
∴DE⊥AB,
∴DE⊥平面ABB1A1,DE?平面ADB1,
∴平面AB1D⊥平面ABB1A1;
(2)连接CO并延长交AB于Q,则Q为AB的中点,连接CP,PQ,
∵点D、P为棱CC1、BB1的中点,
∴PC∥B1D,PQ∥B1A,
∵PC∩PQ=P,B1D∩B1A=B1,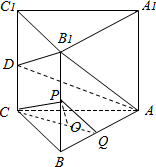
∴平面PQC∥平面AB1D,
∵OP?平面PQC,
∴OP∥平面AB1D.
∵ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,

∴Rt△ACD≌Rt△B1C1D,∴AD=B1D
又E是AB1的中点,∴AB1⊥DE,DE∥CF,
∴DE⊥AB,
∴DE⊥平面ABB1A1,DE?平面ADB1,
∴平面AB1D⊥平面ABB1A1;
(2)连接CO并延长交AB于Q,则Q为AB的中点,连接CP,PQ,
∵点D、P为棱CC1、BB1的中点,
∴PC∥B1D,PQ∥B1A,
∵PC∩PQ=P,B1D∩B1A=B1,

∴平面PQC∥平面AB1D,
∵OP?平面PQC,
∴OP∥平面AB1D.
点评:本题考查面面垂直的判定定理和线面平行判定定理的运用,数量运用判定定理是关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知数列{an}中,a1=1,对所有n∈N*,都有a1a2…an=n2,则a3=( )
A、
| ||
| B、3 | ||
| C、9 | ||
D、
|
分别在区间[1,5]、[1,4]内各任取一个实数依次为m,n,则m>n的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=2x-|x2-1|-1的零点个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知AB是异面直线l1与l2的公垂线段,且AB=3,异面直线l1与l2所成的角为30°,在l1上取AP=6,则点P到l2的距离为( )
| A、6 | ||
B、3
| ||
C、6或3
| ||
D、2
|
 (1)已知矩阵M=
(1)已知矩阵M=