Question

已知O是三角形ABC的外心，AB=2，AC=5，若

AO

=x

AB

+y

AC

，且x+4y=2，则三角形ABC的面积为（　　）

• A、

  5 39

  4

• B、

  5 39

  8

• C、

  5 39

  16

• D、

  5 39

  2

Answer 1

考点：平面向量的基本定理及其意义

专题：平面向量及应用

分析：过外心O分别作OD⊥AB，OE⊥AC，垂足分别为D，E．利用垂经定理可得：AD=

1

2

AB，AE=

1

2

AC．由投影的定义可得：

AO

•

AB

=

1

2

AB

2=2，

AO

•

AC

=

1

2

AC

2=

25

2

．对

AO

=x

AB

+y

AC

分别与

AB

，

AC

作数量积．可得2=4x+10ycosA，

25

2

=10xcosA+25y．又x+4y=2，联立解得cosA．即可得出sinA，利用三角形的面积计算公式即可得出．

解答： 解：如图所示，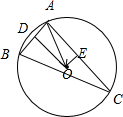
过外心O分别作OD⊥AB，OE⊥AC，垂足分别为D，E．
则AD=

1

2

AB，AE=

1

2

AC．
∴

AO

•

AB

=

1

2

AB

2=2，

AO

•

AC

=

1

2

AC

2=

25

2

．
对

AO

=x

AB

+y

AC

分别与

AB

，

AC

作数量积．
可得：

AO

•

AB

=x

AB

2+y

AB

•

AC

，化为2=4x+10ycosA．

AO

•

AC

=x

AB

•

AC

+y

AC

2，化为

25

2

=10xcosA+25y．
又x+4y=2，
联立解得cosA=

2

5

或

5

8

．
当cosA=

2

5

时，x=0，舍去．
∴cosA=

5

8

．
∴sinA=

1-cos2A

=

39

8

．
∴三角形ABC的面积S=

1

2

AB×ACsinA=

1

2

×2×5×

39

8

=

5 39

8

．
故选：B．

点评：本题综合考查了垂经定理、投影的定义、数量积运算性质、同角三角函数基本关系式、三角形的面积计算公式，考查了推理能力和计算能力，属于难题．