题目内容
设函数f(x)=
,其中[x]表示不超过x的最大整数,如[1.1]=1,[0.3]=0,若函数y=f(x)-k(x+1)恰有三个不同的零点,则k的取值范围是( )
|
A、(-2,-1]∪[
| ||||
B、[-2,-1)∪(0,
| ||||
C、[
| ||||
D、[
|
考点:分段函数的应用
专题:数形结合,函数的性质及应用
分析:根据[x]的定义,求出函数f(x)的表达式,作出函数f(x)和y=k(x+1)的图象,利用数形结合即可得到结论.
解答:
解: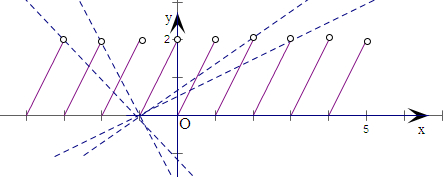 当0≤x<1时,f(x)=2x-2[x]=2x;
当0≤x<1时,f(x)=2x-2[x]=2x;
当1≤x<2,0≤x-1<1,
f(x)=2(x-1)-2[x-1]=
2(x-1);
当2≤x<3,0≤x-2<1,
f(x)=2(x-2);
当3≤x<4,0≤x-3<1,
f(x)=2(x-3);
…
当-1≤x<0,0≤x+1<1,f(x)=2(x+1);
当-2≤x<-1,0≤x+2<1,f(x)=2(x+2);
当-3≤x<-2,0≤x+3<1,f(x)=2(x+3);
当-4≤x<-3,0≤x+4<1,f(x)=2(x+4);
…画出函数f(x)的图象和直线y=k(x+1),
由图象可知,代入(2,2)得,2=3k,k=
;代入(3,2)得,2=4k,得,k=
;
故
<k<
时,f(x)的图象与直线有三个交点;
代入(-2,2)得,2=-k,得,k=-2,代入(-3,2)得,2=-2k,k=-1.
故-2<k<-1时,f(x)的图象与直线有三个交点.
故函数y=f(x)-k(x+1)恰有三个不同的零点,则k的取值范围是(-2,-1)∪(
,
)
 当0≤x<1时,f(x)=2x-2[x]=2x;
当0≤x<1时,f(x)=2x-2[x]=2x;当1≤x<2,0≤x-1<1,
f(x)=2(x-1)-2[x-1]=
2(x-1);
当2≤x<3,0≤x-2<1,
f(x)=2(x-2);
当3≤x<4,0≤x-3<1,
f(x)=2(x-3);
…
当-1≤x<0,0≤x+1<1,f(x)=2(x+1);
当-2≤x<-1,0≤x+2<1,f(x)=2(x+2);
当-3≤x<-2,0≤x+3<1,f(x)=2(x+3);
当-4≤x<-3,0≤x+4<1,f(x)=2(x+4);
…画出函数f(x)的图象和直线y=k(x+1),
由图象可知,代入(2,2)得,2=3k,k=
| 2 |
| 3 |
| 1 |
| 2 |
故
| 1 |
| 2 |
| 2 |
| 3 |
代入(-2,2)得,2=-k,得,k=-2,代入(-3,2)得,2=-2k,k=-1.
故-2<k<-1时,f(x)的图象与直线有三个交点.
故函数y=f(x)-k(x+1)恰有三个不同的零点,则k的取值范围是(-2,-1)∪(
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题主要考查分段函数的应用,以及新定义的理解,利用数形结合是解决本题的关键,综合性较强,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
f(x)=3x+3x-8,且f(1)<0,f(1.5)>0,f(1.25)<0,f(2)>0,则函数f(x)的零点落在区间( )
| A、(1,1.25) |
| B、(1.25,1.5) |
| C、(1.5,2) |
| D、不能确定 |
在梯形ABCD中,AB∥CD,AB=2CD,M、N分别为CD、BC的中点,若
=λ
+μ
,则λ+μ=( )
| AB |
| AM |
| AN |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知O是三角形ABC的外心,AB=2,AC=5,若
=x
+y
,且x+4y=2,则三角形ABC的面积为( )
| AO |
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,| AB |
| a |
| AD |
| b |
| AN |
| NC |
| BN |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,A、B分别是射线OM,ON上的两点,给出下列向量:
如图,A、B分别是射线OM,ON上的两点,给出下列向量: