题目内容
5. 如图,有一个底面是正方形的直棱柱型容器(无盖),底面棱长为1dm(dm为分米),高为5dm,两个小孔在其相对的两条侧棱上,且到下底面距离分别为3dm和4dm,则(水不外漏情况下)此容器可装的水最多为( )
如图,有一个底面是正方形的直棱柱型容器(无盖),底面棱长为1dm(dm为分米),高为5dm,两个小孔在其相对的两条侧棱上,且到下底面距离分别为3dm和4dm,则(水不外漏情况下)此容器可装的水最多为( )| A. | $\frac{9}{2}d{m^3}$ | B. | 4dm3 | C. | $\frac{7}{2}d{m^3}$ | D. | 3dm3 |
分析 由题意,容器可装的水最多时,水面位置为平行四边形ABCD,上面补同样大的几何体,则体积可求.
解答  解:由题意,容器可装的水最多时,水面位置为平行四边形ABCD,
解:由题意,容器可装的水最多时,水面位置为平行四边形ABCD,
上面补同样大的几何体,则体积=$\frac{1}{2}×1×1×7$=$\frac{7}{2}d{m}^{3}$,
故选:C.
点评 本题考查棱柱的结构特征,考查棱柱、棱锥的体积,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.f(x)是定义在(0,+∞)上的单调函数,且对?x∈(0,+∞)都有f(f(x)-lnx)=e+1,则方程f(x)-f′(x)=e的实数解所在的区间是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,e) | D. | (e,4) |
20.二项式(1+2x)4展开式的各项系数的和为( )
| A. | 81 | B. | 80 | C. | 27 | D. | 26 |
17.已知集合M={x|(x-1)=0},那么( )
| A. | 0∈M | B. | 1∉M | C. | -1∈M | D. | 0∉M |
14.已知命题p:若x>10,则x>1,那么p的逆否命题为( )
| A. | 若x>1,则x>10 | B. | 若x>10,则x≤1 | C. | 若x≤10,则x≤1 | D. | 若x≤1,则x≤10 |
15.若平面α截三棱锥所得截面为平行四边形,则该三棱锥与平面α平行的棱有( )
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 1条或2条 |
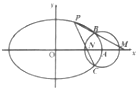 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的长轴长为4,焦距为$2\sqrt{3}$,以A为圆心的圆(x-2)2+y2=r2(r>0)与椭圆相交于B、C两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的长轴长为4,焦距为$2\sqrt{3}$,以A为圆心的圆(x-2)2+y2=r2(r>0)与椭圆相交于B、C两点.