若平面α截三棱锥所得截面为平行四边形.则该三棱锥与平面α平行的棱有( )A．0条B．1条C．2条D．1条或2条题目和参考答案——青夏教育精英家教网—

题目内容

15．若平面α截三棱锥所得截面为平行四边形，则该三棱锥与平面α平行的棱有（　　）

A．

0条

B．

1条

C．

2条

D．

1条或2条

分析利用已知条件，通过直线与平面平行的性质、判定定理，证明CD∥平面EFGH，AB∥平面EFGH，得到结果．

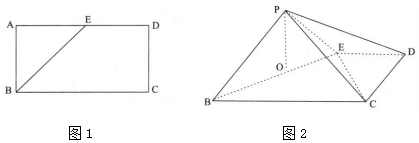
解答解：如图所示，四边形EFGH为平行四边形，则EF∥GH，
∵EF?平面BCD，GH?平面BCD，
∴EF∥平面BCD，
∵EF?平面ACD，平面BCD∩平面ACD=CD，
∴EF∥CD，∴CD∥平面EFGH，
同理AB∥平面EFGH，
故选C．

点评本题主要考查线面平行的判定定理和性质定理的应用．考查对基础知识的综合应用能力和基本定理的掌握能力．

练习册系列答案

相关题目

5．

如图，有一个底面是正方形的直棱柱型容器（无盖），底面棱长为1dm（dm为分米），高为5dm，两个小孔在其相对的两条侧棱上，且到下底面距离分别为3dm和4dm，则（水不外漏情况下）此容器可装的水最多为（　　）

6．已知定义在R上的函数f（x）=|x-m|+|x|，m∈N*，存在实数x使f（x）＜2成立．
（Ⅰ）求正整数m的值；
（Ⅱ）若α＞1，β＞1，f（x）+f（β）=2，求证：$\frac{4}{α}$+$\frac{1}{β}$≥$\frac{9}{2}$．

3．O为△ABC内一点，且2$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=0，△ABC和△OBC的面积分别是S_△ABC和S_△OBC，则$\frac{{S}_{△OBC}}{{S}_{△ABC}}$的比值是$\frac{1}{2}$．

10．已知函数f（x）=sinωx-sin（ωx+$\frac{π}{3}$）（ω＞0）．
（1）若f（x）在[0，π]上的值域为[-$\frac{\sqrt{3}}{2}$，1]，求ω的取值范围；
（2）若f（x）在[0，$\frac{π}{3}$]上单调，且f（0）+f（$\frac{π}{3}$）=0，求ω的值．

20．如图1，矩形ABCD中，AB=1，AD=2，点E为AD中点，沿BE将△ABE折起至△PBE，如图2所示，点P在面BCDE的射影O落在BE上．

（Ⅰ）求证：BP⊥CE；
（Ⅱ）求二面角B-PC-D的余弦值．

7．已知向量$\overrightarrow{a}$=（1，2），向量$\overrightarrow{b}$=（3，-4），则向量$\overrightarrow{a}$在向量$\overrightarrow{b}$方向上的投影为（　　）

4．已知命题p：?x，y∈R，sin（x+y）=sinx+siny，命题$q：?x∈[0，π]，\sqrt{\frac{1+cos2x}{2}}=cosx$，则下列判断正确的是（　　）

	A．	命题p∨q是假命题		B．	命题p∧q是真命题
	C．	命题p∨（￢q）是假命题		D．	命题p∧（￢q）是真命题

4．要得到函数y=sin（2x+$\frac{π}{6}$）的图象，只需将y=cos（2x-$\frac{π}{6}$）图象上的所有点（　　）

	A．	向左平行移动$\frac{π}{6}$个单位长度		B．	向右平行移动$\frac{π}{6}$个单位长度
	C．	向左平行移动$\frac{π}{12}$个单位长度		D．	向右平行移动$\frac{π}{12}$个单位长度

试题分类