题目内容
11.定义在R上的函数f(x),其周期为4,且当x∈[-1,3]时,f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}}}&{x∈[-1,1]}\\{1-|x-2|}&{x∈(1,3]}\end{array}\right.$,(1)画出函数在x∈[-1,3]的简图
(2)若函数g(x)=f(x)-kx-k恰有4个零点,求实数k的取值范围.
分析 (1)根据已知中函数的解析式,可得函数在x∈[-1,3]的简图
(2)若函数g(x)=f(x)-kx-k恰有4个零点,即函数f(x)与y=kx+k的图象有四个交点,数形结合可得答案.
解答 解:(1)∵当x∈[-1,3]时,f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}}}&{x∈[-1,1]}\\{1-|x-2|}&{x∈(1,3]}\end{array}\right.$,
∴函数在x∈[-1,3]的简图如下图: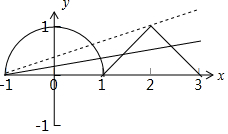
(2)若函数g(x)=f(x)-kx-k恰有4个零点,
即函数f(x)与y=kx+k的图象有四个交点,
由y=kx+k的图象恒过(-1,0)点,
当y=kx+k的图象过(2,1)点时,k=$\frac{1}{3}$,
当y=kx+k的图象与半圆y=$\sqrt{1-(x-4)^{2}}$相切时,k=$\frac{\sqrt{6}}{12}$,
故当k∈($\frac{\sqrt{6}}{12}$,$\frac{1}{3}$)时,即函数f(x)与y=kx+k的图象有四个交点,
即函数g(x)=f(x)-kx-k恰有4个零点.
点评 本题考查的知识点是函数的图象,分段函数的应用,函数的零点,数形结合思想,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知x,y满足$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y≤1}\end{array}\right.$,z=2x+y的最大值为m,若正数a,b满足a+b=m,则$\frac{1}{a}+\frac{4}{b}$的最小值为( )
| A. | 9 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
6.已知集合M={x|lg(x-2)≤0},P={y|-1≤y≤3},则M∩P=( )
| A. | ∅ | B. | {x|2<x<3} | C. | M | D. | {x|x≤3} |
3.已知函数 $f(x)={2^x}-\sqrt{x}-14$,若在区间(0,16)内随机取一个数x0,则f(x0)>0的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
1.在△ABC中,a、b、c分别为角A、B、C所对的边,且a=2,b=$\sqrt{6}$,B=$\frac{π}{3}$,则角A等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |