题目内容
20．已知sinx+$\sqrt{3}$cosx=$\frac{8}{5}$，则sin（x+$\frac{π}{3}$）=$\frac{4}{5}$．分析 推导出2sin（x+$\frac{π}{3}$）=$\frac{8}{5}$，由此能求出sin（x+$\frac{π}{3}$）的值．
解答 解：∵sinx+$\sqrt{3}$cosx=$\frac{8}{5}$，
∴2sin（x+$\frac{π}{3}$）=$\frac{8}{5}$，
∴sin（x+$\frac{π}{3}$）=$\frac{4}{5}$．
故答案为：$\frac{4}{5}$．
点评 本题考查正弦函数值的求法，是基础题，解题时要认真审题，注意三角函数性质的合理运用．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
18．下列命题正确的是（ ）
| A． | 命题“$?{x_0}∈R，{x_0}^2+1＞3{x_0}$”的否定是“$?{x_0}∈R，{x^2}+1＞3x$” | |
| B． | “函数f（x）=cosax-sinax的最小正周期为 π”是“a=2”的必要不充分条件 | |
| C． | x2+2x≥ax在x∈[1，2]时有解?（x2+2x）min≥（ax）min在x∈[1，2]时成立 | |
| D． | “平面向量$\overrightarrow a$与$\overrightarrow b$的夹角是钝角”的充分必要条件是“$\overrightarrow a$•$\overrightarrow b$＜0” |
15．
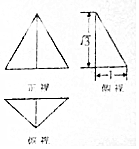已知三棱锥的三视图如图所示，其中俯视图为直角三角形，俯视图为等腰直角三角形，则此三棱锥的体积等于（ ）
已知三棱锥的三视图如图所示，其中俯视图为直角三角形，俯视图为等腰直角三角形，则此三棱锥的体积等于（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\sqrt{3}$ |
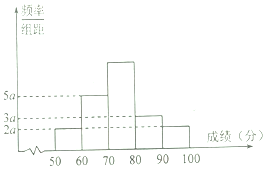某学习小组20名学生一次数学考试成绩（单位：分）频率直方图如图所示，已知前三个矩形框垂直于横轴的高度成等差数列．