题目内容
3．已知函数 $f（x）={2^x}-\sqrt{x}-14$，若在区间（0，16）内随机取一个数x0，则f（x0）＞0的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
分析 由题意可得总的区间长度，解不等式可得满足条件的区间长度，由几何概型的概率公式可得．
解答 解：令f（x）=0，解得：x=4，
故在区间（0，16）内随机取一个数x0，则f（x0）＞0的概率
p=$\frac{16-4}{16}$=$\frac{3}{4}$，
故选：D．
点评 本题考查几何概型，涉及不等式的解法，属基础题．
练习册系列答案
相关题目
1．双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$右焦点到渐近线的距离为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | $\frac{12}{5}$ |
18．已知集合 A={-2，-1，0，2，3}，B={y|y=|x|，x∈A}，则A∩B=（ ）
| A． | {0，1，2，3} | B． | {2，3} | C． | {0，1，2} | D． | {0，2，3} |
15．
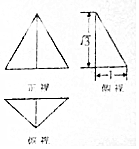已知三棱锥的三视图如图所示，其中俯视图为直角三角形，俯视图为等腰直角三角形，则此三棱锥的体积等于（ ）
已知三棱锥的三视图如图所示，其中俯视图为直角三角形，俯视图为等腰直角三角形，则此三棱锥的体积等于（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\sqrt{3}$ |