题目内容

1．在△ABC中，a、b、c分别为角A、B、C所对的边，且a=2，b=$\sqrt{6}$，B=$\frac{π}{3}$，则角A等于（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{3π}{4}$D．$\frac{π}{4}$或$\frac{3π}{4}$

分析 由正弦定理可得$\frac{2}{sinA}$=$\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}$，结合a＜b，即可得出结论．

解答 解：由正弦定理可得$\frac{2}{sinA}$=$\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}$，∴sinA=$\frac{\sqrt{2}}{2}$，
∵a＜b，∴A=$\frac{π}{4}$．
故选B．

点评 本题考查正弦定理，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
11．定义在R上的函数f（x），其周期为4，且当x∈[-1，3]时，f（x）=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}}}&{x∈[-1，1]}\\{1-|x-2|}&{x∈（1，3]}\end{array}\right.$，
（1）画出函数在x∈[-1，3]的简图
（2）若函数g（x）=f（x）-kx-k恰有4个零点，求实数k的取值范围．
12．已知{an}是公差不为0的等差数列，a1=1，且a1，a3，a9成等比数列．
（1）求数列{an}的通项公式；
（2）若bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$，求证：数列{bn}的前n项和Sn＜1．
9．给出下列结论：
①已知函数f（x）是定义在R上的奇函数，若f（-1）=2，f（-3）=-1，则f（3）＜f（-1）；
②函数y=log${\;}_{\frac{1}{2}}$（x2-2x）的单调递增减区间是（-∞，0）；
③已知函数f（x）是奇函数，当x≥0时，f（x）=x2，则当x＜0时，f（x）=-x2；
④若函数y=f（x）的图象与函数y=ex的图象关于直线y=x对称，则对任意实数x，y都有f（xy）=f（x）+f（y）．
则正确结论的序号是①③④（请将所有正确结论的序号填在横线上）．
16．已知函数f（x）=axlnx，x∈（0，+∞），其中a为实数，f′（x）为f（x）的导函数，若f′（1）=2，则a的值为2．
6．已知等比数列{an}的公比为正数，且a1•a7=2a32，a2=2，则a1的值是$\sqrt{2}$．
13．已知等差数列{an}的前n项和为Sn，公差d≠0，且S1+S3=18，a1，a4，a13成等比数列．
（1）求数列{an}的通项公式；
（2）设{$\frac{{a}_{n}}{{b}_{n}}$}是首项为1，公比为$\frac{1}{3}$的等比数列，求数列{bn}前n项和Tn．
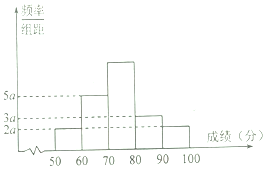10．某学习小组20名学生一次数学考试成绩（单位：分）频率直方图如图所示，已知前三个矩形框垂直于横轴的高度成等差数列．
（1）求频率分布直方图中a的值；
（2）分别求出成绩落在[50，60）与[80，90）中的学生人数；
（3）从成绩在[50，60）与[80，90）中的学生中人选2人，求此2人的成绩相差20分以上的概率．
11．设命题p：?x0∈（-2，+∞），6+|x0|=5．命题q：?x∈（-∞，0），x2+$\frac{4}{{x}^{2}}$≥4．命题r：若|x|+|y|≤1，则$\frac{|y|}{|x|+2}$≤$\frac{1}{2}$．
（1）写出命题r的否命题；
（2）判断命题￢p，p∨r，p∧q的真假，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网