题目内容
6．设集合A={x|log2（x+1）＜2}，B={y|y=$\sqrt{16-{2}^{x}}$}，则（∁RA）∩B=（ ）| A． | （0，3） | B． | [0，4] | C． | [3，4） | D． | （-1，3） |
分析 求出集合的等价条件，根据集合的基本运算进行求解即可．
解答 解：A={x|log2（x+1）＜2}={x|0＜x+1＜4}={x|-1＜x＜3}，
则∁RA={x|x≥3或x≤-1}，
B={y|y=$\sqrt{16-{2}^{x}}$}={y|0≤y＜4}，
则（∁RA）∩B={x|3≤x＜4}=[3，4），
故选：C．
点评 本题主要考查集合的基本运算，求出集合的等价条件是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
9．等差数列{an}的公差为2，若a2，a4，a8成等比数列，设Sn是数列{an}的前n项和，则S10的值为（ ）
| A． | 110 | B． | 90 | C． | 55 | D． | 45 |
10．
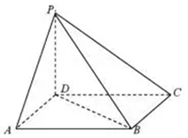如图，四棱锥P-ABCD中，PD⊥底面ABCD，且底面ABCD为平行四边形，若∠DAB=60°，AB=2，AD=1．
（1）求证：PA⊥BD；
（2）若∠PCD=45°，求点D到平面PBC的距离h．
如图，四棱锥P-ABCD中，PD⊥底面ABCD，且底面ABCD为平行四边形，若∠DAB=60°，AB=2，AD=1．（1）求证：PA⊥BD；
（2）若∠PCD=45°，求点D到平面PBC的距离h．
11．已知函数f（x）=4ex（x+1）-k（$\frac{2}{3}$x3+2x2），若x=-2是函数f（x）的唯一一个极值点，则实数k的取值范围是（ ）
| A． | （-2e，e] | B． | [0，2e] | C． | （-∞，-e）∪[e，2e] | D． | （-∞，-e）∪[0，e] |
15．某班主任对班级90名学生进行了作业量多少的调查，结合数据建立了下列列联表：
利用独立性检验估计，你认为推断喜欢电脑游戏与认为作业多少有关系错误的概率介于（ ）
（观测值表如下）
| 认为作业多 | 认为作业少 | 总计 | |
| 喜欢玩电脑游戏 | 10 | 35 | 45 |
| 不喜欢玩玩电脑游戏 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
（观测值表如下）
| P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 |
| A． | 0.15～0.25 | B． | 0.4～0.5 | C． | 0.5～0.6 | D． | 0.75～0.85 |