题目内容
10.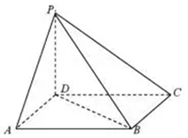 如图,四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1.(1)求证:PA⊥BD;
(2)若∠PCD=45°,求点D到平面PBC的距离h.
分析 (1)利用勾股定理逆定理证明AD⊥BD,结合BD⊥PD得出BD⊥平面PAD,故而PA⊥BD;
(2)根据VP-BCD=VD-BCP列方程解出h.
解答 (1)证明:∵AD=1,AB=2,∠DAB=60°,
∴BD2=AB2+AD2-2AB•AD•cos60°=3,
∴AD2+BD2=AB2,
∴AD⊥BD,
∵PD⊥平面ABCD,BD?平面ABCD,
∴PD⊥BD,又AD∩PD=D,
∴BD⊥平面PAD,
∵PA?平面PAD,
∴BD⊥PA.
(2)解:由(1)可知BC⊥BD,
∴S△BCD=$\frac{1}{2}×BC×BD$=$\frac{\sqrt{3}}{2}$,
∵∠PCD=45°,∴PD=CD=2,
∴VP-BCD=$\frac{1}{3}×\frac{\sqrt{3}}{2}×2$=$\frac{\sqrt{3}}{3}$.
∵PC=$\sqrt{2}$CD=2$\sqrt{2}$,PB=$\sqrt{P{D}^{2}+D{B}^{2}}$=$\sqrt{7}$,BC=1,
∴BC2+PB2=PC2,∴PB⊥BC,
∴S△BCP=$\frac{1}{2}BC•PB$=$\frac{\sqrt{7}}{2}$,
∴VD-BCP=$\frac{1}{3}×\frac{\sqrt{7}}{2}×h$=$\frac{\sqrt{7}h}{6}$,
又VP-BCD=VD-BCP,∴$\frac{\sqrt{7}h}{6}$=$\frac{\sqrt{3}}{3}$,
解得h=$\frac{2\sqrt{21}}{7}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.设集合$A=\left\{{({x,y})|\frac{x^2}{4}+\frac{y^2}{16}=1}\right\}$,B={(x,y)|y=3x},则A∩B的子集的个数是( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
1.已知点P在抛物线y=x2上,点Q在圆(x-4)2+(y+$\frac{1}{2}$)2=1上,则|PQ|的最小值为( )
| A. | $\frac{3\sqrt{5}}{2}$-1 | B. | $\frac{3\sqrt{3}}{2}$-1 | C. | 2$\sqrt{3}$-1 | D. | $\sqrt{10}$-1 |
9.曲线y=ex+x在点(0,1)处的切线方程为( )
| A. | x+y-1=0 | B. | 2x-y+1=0 | C. | 2x+y-1=0 | D. | x-y+1=0 |
6.设集合A={x|log2(x+1)<2},B={y|y=$\sqrt{16-{2}^{x}}$},则(∁RA)∩B=( )
| A. | (0,3) | B. | [0,4] | C. | [3,4) | D. | (-1,3) |
7.为了解某种产品的月广告费用x(单位:万元)对月销售量y(单位:万台)的影响,收集到如下5个月的统计数据:
根据上表中的数据可得线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=4.2,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,据此估计,该产品的月广告费为13万元时的月销售量为( )
| 广告费x(万元) | 1 | 2 | 3 | 4 | 5 |
| 销售量y(万台) | 2 | 5 | 10 | 15 | 18 |
| A. | 30 | B. | 52 | C. | 57.2 | D. | 70 |