题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{3x+5,(x<1)}\\{lo{g}_{\frac{1}{2}}x-1,(x≥1)}\end{array}\right.$,则f(f(2$\sqrt{2}$))=-$\frac{5}{2}$.分析 先求出f(2$\sqrt{2}$)=$lo{g}_{\frac{1}{2}}2\sqrt{2}$-1=-$\frac{5}{2}$,从而f(f(2$\sqrt{2}$))=f(-$\frac{5}{2}$)=3×(-$\frac{5}{2}$)+5,由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{3x+5,(x<1)}\\{lo{g}_{\frac{1}{2}}x-1,(x≥1)}\end{array}\right.$,
∴f(2$\sqrt{2}$)=$lo{g}_{\frac{1}{2}}2\sqrt{2}$-1=-$\frac{3}{2}-1=-\frac{5}{2}$,
f(f(2$\sqrt{2}$))=f(-$\frac{5}{2}$)=3×(-$\frac{5}{2}$)+5=-$\frac{5}{2}$.
故答案为:-$\frac{5}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
1.已知点P在抛物线y=x2上,点Q在圆(x-4)2+(y+$\frac{1}{2}$)2=1上,则|PQ|的最小值为( )
| A. | $\frac{3\sqrt{5}}{2}$-1 | B. | $\frac{3\sqrt{3}}{2}$-1 | C. | 2$\sqrt{3}$-1 | D. | $\sqrt{10}$-1 |
9.曲线y=ex+x在点(0,1)处的切线方程为( )
| A. | x+y-1=0 | B. | 2x-y+1=0 | C. | 2x+y-1=0 | D. | x-y+1=0 |
6.设集合A={x|log2(x+1)<2},B={y|y=$\sqrt{16-{2}^{x}}$},则(∁RA)∩B=( )
| A. | (0,3) | B. | [0,4] | C. | [3,4) | D. | (-1,3) |
13.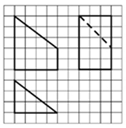 如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
 如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
3.现要给一长、宽、高分别为3、2、1的长方体工艺品各面涂色,有红、橙、黄、蓝、绿五种颜色的涂料可供选择,要求相邻的面不能涂相同的颜色,且橙色跟黄色二选一,红色要涂两个面,则不同的涂色方案种数有( )
| A. | 48种 | B. | 72种 | C. | 96种 | D. | 108种 |
7.为了解某种产品的月广告费用x(单位:万元)对月销售量y(单位:万台)的影响,收集到如下5个月的统计数据:
根据上表中的数据可得线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=4.2,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,据此估计,该产品的月广告费为13万元时的月销售量为( )
| 广告费x(万元) | 1 | 2 | 3 | 4 | 5 |
| 销售量y(万台) | 2 | 5 | 10 | 15 | 18 |
| A. | 30 | B. | 52 | C. | 57.2 | D. | 70 |
8.设集合A={x|x2-4x+3<0},U={x|x-1>0},则∁UA=( )
| A. | (3,+∞) | B. | [3,+∞) | C. | (1,3) | D. | (1,+∞) |