题目内容
1.已知函数f(x)=$\frac{1}{2}$x2-2aln x+(a-2)x,a∈R.(1)当a=1时,求函数f(x)的图象在点(1,f(1))处的切线方程;
(2)是否存在实数a,对任意的x1,x2∈(0,+∞)且x1≠x2有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$>a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
分析 (1)求出函数的导数,计算f′(1)的值,求出切线方程即可;
(2)令g(x)=f(x)-ax=$\frac{1}{2}$x2-2alnx-2x,根据函数的单调性得到2a≤x2-2x=(x-1)2-1在(0,+∞)上恒成立,求出a的范围即可.
解答 解:(1)函数f(x)=$\frac{1}{2}$x2-2aln x+(a-2)x,定义域是(0,+∞),
所以f′(x)=$\frac{(x-2)(x+a)}{x}$,(x>0),
当a=1时,f′(x)=$\frac{(x-2)(x+1)}{x}$,所以f′(1)=-2,
则所求切线方程为y-f(1)=-2(x-1),即4x+2y-3=0;
(2)假设存在这样的实数a满足条件,不妨设0<x1<x2,
由$\frac{f{(x}_{2})-f{(x}_{1})}{{x}_{2}{-x}_{1}}$>a,知f(x2)-ax2>f(x1)-ax1成立,
令g(x)=f(x)-ax=$\frac{1}{2}$x2-2alnx-2x,
则函数g(x)在(0,+∞)上单调递增,
则g′(x)=x-$\frac{2a}{x}$-2≥0,即2a≤x2-2x=(x-1)2-1在(0,+∞)上恒成立,
则a≤-$\frac{1}{2}$,故存在这样的实数a满足题意,
其取值范围为(-∞,-$\frac{1}{2}$].
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
9.曲线y=ex+x在点(0,1)处的切线方程为( )
| A. | x+y-1=0 | B. | 2x-y+1=0 | C. | 2x+y-1=0 | D. | x-y+1=0 |
6.设集合A={x|log2(x+1)<2},B={y|y=$\sqrt{16-{2}^{x}}$},则(∁RA)∩B=( )
| A. | (0,3) | B. | [0,4] | C. | [3,4) | D. | (-1,3) |
13.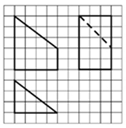 如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
 如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
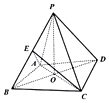 如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP中点,AC与BD交于点O,且OP⊥平面ABCD.
如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP中点,AC与BD交于点O,且OP⊥平面ABCD.