题目内容
已知函数y=f(x+1)为奇函数,y=f(x-1)为偶函数,且f(0)=1,则f(4)= .
考点:函数奇偶性的性质,函数单调性的性质,函数的值
专题:函数的性质及应用
分析:利用y=f(x+1)为奇函数,y=f(x-1)为偶函数,将f(4)进行转化即可.
解答:
解:∵y=f(x+1)为奇函数,y=f(x-1)为偶函数,
∴f(-x+1)=-f(x+1),①
f(-x-1)=f(x-1),②
即函数f(x)关于x=-1对称.
∴f(x-1)=f(-x-1)②
在②中令x=1得:f(0)=f(-2)=1,
∴f(-2)=1,
在①中令x=-3得:f(-2)=-f(4),
∴f(4)=-f(-2)=-1,
答案为:-1.
∴f(-x+1)=-f(x+1),①
f(-x-1)=f(x-1),②
即函数f(x)关于x=-1对称.
∴f(x-1)=f(-x-1)②
在②中令x=1得:f(0)=f(-2)=1,
∴f(-2)=1,
在①中令x=-3得:f(-2)=-f(4),
∴f(4)=-f(-2)=-1,
答案为:-1.
点评:本题主要考查函数奇偶性的应用,利用函数奇偶性的性质,将f(4)进行转化是解决本题的关键.

练习册系列答案
相关题目
不论m为何值,直线(m-1)x+(2m-1)y=m-5恒过定点( )
A、(1,-
| ||
| B、(-2,0) | ||
| C、(2,3) | ||
| D、(9,-4) |
两条不重合的直线l1和l2的方向向量分别为
=(1,-1,2),
=(0,2,1),则l1与l2的位置关系是( )
| v1 |
| v2 |
| A、平行 | B、相交 | C、垂直 | D、不确定 |
不等式x2-3x+2>0的解集是( )
| A、∅ |
| B、R |
| C、(1,2) |
| D、(-∞,1)∪(2,+∞) |
将一个水平放置的正方形ABCD绕直线AB向上转动45°到ABC1D1,再将所得正方形ABC1D1绕直线BC1向上转动45°到A2BC1D2,则平面A2BC1D2与平面ABCD所成二面角的正弦值等于 .
设a=log
3,b=(
)0.2,c=2
,则( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、a>b>c |
| B、b>a>c |
| C、b>c>a |
| D、c>b>a |
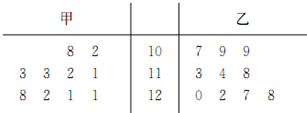 为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)
为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)