题目内容
已知⊙O:(x-3)2+(y+1)2=25的圆心为O,过点A(1,2)的直线l与⊙O相交于A,B两点,当点O到直线l的距离最大时,弦AB的长为 .
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:当点O到直线l的距离最大时,OA⊥直线l,利用勾股定理,即可得出结论.
解答:
解:当点O到直线l的距离最大时,OA⊥直线l,
∵OA=
=
,
∴弦AB的长为2
=4
,
故答案为:4
∵OA=
| (3-1)2+(-1-2)2 |
| 13 |
∴弦AB的长为2
| 25-13 |
| 3 |
故答案为:4
| 3 |
点评:本题考查直线与圆相交的性质,考查勾股定理,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将边长为a的正方形沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
登上一个四级的台阶,可以选择的方式共有( )种.
| A、3 | B、4 | C、5 | D、8 |
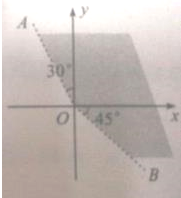 如图,终边落在OA位置的角α的集合是
如图,终边落在OA位置的角α的集合是


