题目内容
4.设函数f(x)=ax+3-|2x-1|.(Ⅰ)若a=1,解不等式f(x)≤2;
(Ⅱ)若函数有最大值,求a的取值范围.
分析 (Ⅰ)需要去掉绝对值,得到不等式解得即可,
(Ⅱ)把含所有绝对值的函数,化为分段函数,再根据函数f(x)有最大值的充要条件,即可求得.
解答 解:(Ⅰ)由题意得x≥$\frac{1}{2}$时,不等式化为x+3-3x+1≤2,
解得:x≥2,
x<$\frac{1}{2}$时,不等式化为x+3+2x-1≤2,解得:x≤0,
综上,不等式的解集是(-∞,0]∪[2,+∞);
(Ⅱ)由题意得f(x)=$\left\{\begin{array}{l}{(a+2)x+2,x<\frac{1}{2}}\\{(a-2)x+4,x≥\frac{1}{2}}\end{array}\right.$,
函数有最大值的充要条件是a+2≥0且a-2≤0,
即-2≤a≤2.
点评 本题主要考查含有绝对值不等式的解法,关键是去绝对值,需要分类讨论,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
12.若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为$\frac{π}{3}$的两个单位向量,则$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$;$\overrightarrow{b}$=-3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
19.若集合A={x|-1<x<2},B={x|2x2-5x-3>0},则A∩B=( )
| A. | {x|-1<x<-$\frac{1}{2}$,或2<x<3} | B. | {x|2<x<3} | ||
| C. | {x|-$\frac{1}{2}$<x<2} | D. | {x|-1<x<-$\frac{1}{2}$} |
9.已知集合A={x|x2-x-6>0),B={x|-1≤x≤4),则A∩B=( )
| A. | [-l,3) | B. | (3,4] | C. | [-1,2) | D. | (2,4] |
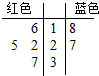 袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示:
袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示: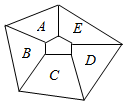 如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )
如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )