题目内容
16.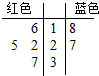 袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示:
袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示:(Ⅰ)从以上六张卡片中任取两张,求这两张卡片颜色相同的概率;
(Ⅱ)从以上六张卡片中任取两张,求这两张卡片数字之和小于50的概率.
分析 (Ⅰ)从以上六张卡片中任取两张,先求出基本事件数,再求出这两张卡片颜色相同包含的基本事件个数,由此能求出这两张卡片颜色相同的概率.
(Ⅱ)从以上六张卡片中任取两张,先求出基本事件数,再利用列举法求出这两张卡片数字之和小于50,包含的基本事件个数,由此能求出这两张卡片数字之和小于50的概率.
解答 解:(Ⅰ)从以上六张卡片中任取两张,基本事件数n=${C}_{6}^{2}$=15,
这两张卡片颜色相同包含的基本事件个数m=${C}_{4}^{2}+{C}_{2}^{2}$=7,
∴这两张卡片颜色相同的概率p=$\frac{7}{15}$.
(Ⅱ)从以上六张卡片中任取两张,基本事件数n=${C}_{6}^{2}$=15,
这两张卡片数字之和小于50,包含的基本事件有:(16,18),(16,27),(16,22),
(16,25),(22,18),(25,18),(27,18),(22,25),(22,27),共9个,
∴这两张卡片数字之和小于50的概率p=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式、列举法的性质的合理运用.

练习册系列答案
相关题目
6.若sinx-2cosx=$\sqrt{5}$,则tanx=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
11.执行如图所示的程序框图,欲使输出的S>11,则输入整数n的最小值为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |