题目内容
已知函数f(x)=b•ax,(其中a,b为常数且a>0,a≠1)的图象经过点A(1,8),B(3,32)
(1)求f(x)的解析式;
(2)若不等式(
)x+(
)x+1-2m≥0在x∈(-∞,1]上恒成立,求实数m的取值范围.
(1)求f(x)的解析式;
(2)若不等式(
| 1 |
| a |
| 1 |
| b |
考点:其他不等式的解法,函数解析式的求解及常用方法
专题:不等式的解法及应用
分析:(1)把点A(1,8),B(3,32)代入函数f(x)=b•ax,求得a、b的值,可得f(x)的解析式.
(2)不等式即 m≤
•[(
)x]2+
•(
)x+
,令t=(
)x,则 m≤
•t2+
t+
.利用二次函数的性质求得g(t)=
•t2+
t+
的最小值,可得m的范围.
(2)不等式即 m≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)把点A(1,8),B(3,32)代入函数f(x)=b•ax,可得
,求得
,∴f(x)=4•2x.
(2)不等式(
)x+(
)x+1-2m≥0,即 m≤
•[(
)x]2+
•(
)x+
.
令t=(
)x,则 m≤
•t2+
t+
.
记g(t)=
•t2+
t+
=
•(t+
)2+
,由x∈(-∞,1],可得t≥
.
故当t=
时,函数g(t)取得最小值为
.
由题意可得,m≤g(t)min,∴m≤
.
|
|
(2)不等式(
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令t=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
记g(t)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 2 |
故当t=
| 1 |
| 2 |
| 7 |
| 8 |
由题意可得,m≤g(t)min,∴m≤
| 7 |
| 8 |
点评:本题主要考查用待定系数法求函数的解析式,函数的恒成立问题,二次函数的性质应用,属于基础题.

练习册系列答案
相关题目
下列命题中是真命题的是( )
| A、任何实数都有算术平方根 |
| B、存在三个实数,它们的和与积相等 |
| C、椭圆的离心率e越接近1时越扁,当e=1时为线段F2F2 |
| D、任意一个无理数,其平方后仍为无理数 |
若平面向量
与
=(1,-2)的夹角是180°,且|
|=3
,则
等于( )
| a |
| b |
| a |
| 5 |
| a |
| A、.(6,-3) |
| B、(3,-6) |
| C、(-3,6) |
| D、(-6,3) |
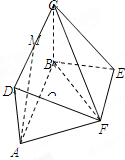 如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.
如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.