题目内容
若原点在直线l上的射影为（2，-1），则l的斜率（ ）
| A、3 | ||
| B、2 | ||
C、-
| ||
| D、-1 |
考点：直线的斜率
专题：直线与圆
分析：由原点O在直线l上的射影为M（2，-1），可得OM⊥l，求出OM的斜率后再根据两直线垂直和斜率间的关系得答案．
解答：
解：∵原点O在直线l上的射影为M（2，-1），
则OM⊥l，kOM=-
，
∴直线l的斜率为OM所在直线斜率的负倒数等于2．
故选：B．
则OM⊥l，kOM=-
| 1 |
| 2 |
∴直线l的斜率为OM所在直线斜率的负倒数等于2．
故选：B．
点评：本题考查了直线的斜率，考查了两直线垂直与斜率间的关系，是基础题．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知函数f（x）=
，则f（f（2））=（ ）
|
A、
| ||
B、
| ||
| C、2 | ||
| D、-2 |
若点P（-m，4）是角α终边上一点，且cosα=-
，则m的值为（ ）
| 3 |
| 5 |
| A、3 | B、-3 | C、±3 | D、5 |
下列各组函数中，是同一函数的是（ ）
A、y=2x+1与y=
| ||
B、f（x）=x与g（x）=
| ||
C、y=
| ||
| D、y=3x2+2x+1与u=3y2+2y+1 |
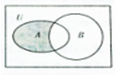
设全集U=R，A={x||x-1|＜1}，B={x|y=
}，则图中阴影部分表示的集合是（ ）
| 1 | ||
|
| A、{x|x≥1} |
| B、{x|1≤x＜2} |
| C、{x|0＜x≤1} |
| D、{x|1≤1} |
从区间（-3，3）中任取两个整数a，b，设点（a，b）在圆x2+y2=3内的概率为 P1，从区间（-3，3）中任取两个实数a，b，直线ax+by+3=0和圆x2+y2=3相离的概率为 P2，则（ ）
| A、P1＞P2 |
| B、P1＜P2 |
| C、P1=P2 |
| D、P1和 P2的大小关系无法确定 |