题目内容
已知点P(x,y)是平面区域
内的动点,点A(1,-1),O为坐标原点,设|
-
|(λ∈R)的最小值为M,若M≤
恒成立,则实数m的取值范围是( )
|
| OP |
| λOA |
| 2 |
A、[-
| ||||
B、(-∞,-
| ||||
C、[-
| ||||
D、[-
|
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:分m>0,m=0,m<0三种情况作可行域,然后分析使|
-
|取最小值时的P点在可行域内的位置,由M≤
得到m的取值范围.
| OP |
| λOA |
| 2 |
解答:
解:直线x=m(y-4)恒过定点(0,4),
当m>0时,由约束条件
作可行域如图,
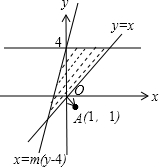
|
-
|的最小值为M=0,满足M≤
;
当m=0时,直线x=m(y-4)与y轴重合,平面区域
为图中y轴右侧的阴影区域,
|
-
|的最小值为M=0,满足M≤
;
当m<0时,由约束条件
作可行域如图阴影部分,
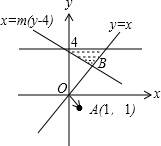
当P点与B重合时,|
-
|(λ∈R)的最小值M=|
|,
联立
,解得B(
,
).
|
|=
|
|,
由
|
|≤
,解得:-
≤m≤
.
∴-
≤m<0.
综上,实数m的取值范围是[-
,+∞).
故选:C.
当m>0时,由约束条件
|

|
| OP |
| λOA |
| 2 |
当m=0时,直线x=m(y-4)与y轴重合,平面区域
|
|
| OP |
| λOA |
| 2 |
当m<0时,由约束条件
|

当P点与B重合时,|
| OP |
| λOA |
| OB |
联立
|
| 4m |
| m-1 |
| 4m |
| m-1 |
|
| OB |
| 2 |
| 4m |
| m-1 |
由
| 2 |
| 4m |
| m-1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
∴-
| 1 |
| 3 |
综上,实数m的取值范围是[-
| 1 |
| 3 |
故选:C.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法及分类讨论的数学思想方法,关键是对题意的理解,是难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、命题“若x2=1,x=1”的否命题是“若x2=1,则x≠1” | ||
| B、“x=-1”是“x2-x-2=0”的必要不充分条件 | ||
| C、命题“若x=y,则sinx=siny”的逆否命题是真命题 | ||
D、“tanx=1”是“x=
|
已知x<-3,则下列关于函数f(x)=x+
的说法正确的是( )
| 4 |
| x+3 |
| A、有最大值-7 |
| B、有最小值-7 |
| C、有最大值4 |
| D、有最小值-4 |
已知x,y满足x≥0,x2+(y-2)2=2,则w=
的最大值为( )
| 3x2+2xy+3y2 |
| x2+y2 |
| A、4 | B、5 | C、6 | D、7 |
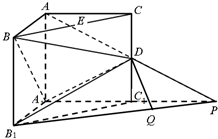 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.