题目内容
已知x＜-3，则下列关于函数f（x）=x+
的说法正确的是（ ）
| 4 |
| x+3 |
| A、有最大值-7 |
| B、有最小值-7 |
| C、有最大值4 |
| D、有最小值-4 |
考点：基本不等式
专题：不等式的解法及应用
分析：变形利用基本不等式即可得出．
解答：
解：∵x＜-3，
∴函数f（x）=x+
=-[-(x+3)+
]-3≤-2
-3=-7，当且仅当x=-5时取等号．
此时函数f（x）取得最大值-7．
故选：A．
∴函数f（x）=x+
| 4 |
| x+3 |
| 4 |
| -(x+3) |
-(x+3)•
|
此时函数f（x）取得最大值-7．
故选：A．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设f（
）=x，则f′（x）=（ ）
| 1 |
| x |
| A、1 | ||
B、
| ||
C、-
| ||
| D、2x |
已知点P（x，y）是平面区域
内的动点，点A（1，-1），O为坐标原点，设|
-
|（λ∈R）的最小值为M，若M≤
恒成立，则实数m的取值范围是（ ）
|
| OP |
| λOA |
| 2 |
A、[-
| ||||
B、（-∞，-
| ||||
C、[-
| ||||
D、[-
|
设U=R，若集合M={x|-1＜x≤2}，则∁UM=（ ）
| A、（-∞，-1] |
| B、（2，+∞） |
| C、（-∞，-1]∪[2，+∞） |
| D、（-∞，-1]∪（2，+∞） |
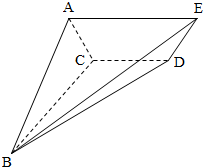如图，四棱锥B-ACDE中，底面ACDE为直角梯形，CD∥AE，∠BCD=∠ACD=90°，二面角A-CD-B为60°，AE=BC=2，AC=CD=1．