题目内容
在△ABC中，角A、B、C的对边分别为a，b，c，且满足（2c-a）cosB-bcosA=0．
（1）求角B的大小；
（2）若a+c=6，b=2
，求△ABC的面积．
（1）求角B的大小；
（2）若a+c=6，b=2
| 3 |
考点：正弦定理
专题：三角函数的求值
分析：（1）已知等式利用正弦定理化简，整理后根据sinC不为0求出cosB的值，即可确定出B的度数；
（2）利用余弦定理列出关系式，将b，cosB的值代入得到关系式，记作①，再由a+c=6，两边平方利用完全平方公式展开得到关系式，记作②，联立①②求出ac的值，再由sinB的值，利用三角形的面积公式即可求出三角形ABC的面积．
（2）利用余弦定理列出关系式，将b，cosB的值代入得到关系式，记作①，再由a+c=6，两边平方利用完全平方公式展开得到关系式，记作②，联立①②求出ac的值，再由sinB的值，利用三角形的面积公式即可求出三角形ABC的面积．
解答：
解：（1）已知等式利用正弦定理化简得：（2sinC-sinA）cosB-sinBsinA=0，
∴2sinCcosB-（sinAcosB+cosAsinB）=2sinCcosB-sin（A+B）=2sinCcosB-sinC=0，
∵sinC≠0，
∴cosB=
，
则B=
；
（2）∵cosB=
，b=2
，
∴由余弦定理得：b2=a2+c2-2accosB，即a2+c2-ac=12①，
∵a+c=6，
∴（a+c）2=a2+c2+2ac=36②，
联立①②得：ac=8，
则S△ABC=
acsinB=2
．
∴2sinCcosB-（sinAcosB+cosAsinB）=2sinCcosB-sin（A+B）=2sinCcosB-sinC=0，
∵sinC≠0，
∴cosB=
| 1 |
| 2 |
则B=
| π |
| 3 |
（2）∵cosB=
| 1 |
| 2 |
| 3 |
∴由余弦定理得：b2=a2+c2-2accosB，即a2+c2-ac=12①，
∵a+c=6，
∴（a+c）2=a2+c2+2ac=36②，
联立①②得：ac=8，
则S△ABC=
| 1 |
| 2 |
| 3 |
点评：此题考查了正弦、余弦定理，三角形的面积公式，熟练掌握公式及定理是解本题的关键．
练习册系列答案
相关题目
已知点P（x，y）是平面区域
内的动点，点A（1，-1），O为坐标原点，设|
-
|（λ∈R）的最小值为M，若M≤
恒成立，则实数m的取值范围是（ ）
|
| OP |
| λOA |
| 2 |
A、[-
| ||||
B、（-∞，-
| ||||
C、[-
| ||||
D、[-
|
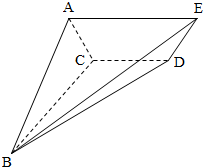如图，四棱锥B-ACDE中，底面ACDE为直角梯形，CD∥AE，∠BCD=∠ACD=90°，二面角A-CD-B为60°，AE=BC=2，AC=CD=1．
在直三棱柱ABC-A′B′C′中，AB⊥AC，D，E分别是BC，A′B′的中点，AB=AC=2，AA′=4．