题目内容
王明早晨在6:30~7:00之间离开家去上学,送奶员在早上6:45~7:15之把牛奶送到王明家,则王明离开家之前能取到牛奶的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:根据题意,设送报人到达的时间为x,小明爸爸离家去工作的时间为y;则(x,y)可以看成平面中的点,分析可得由试验的全部结果所构成的区域并求出其面积,同理可得事件A所构成的区域及其面积,由几何概型公式,计算可得答案.
解答:
 解:设送奶员到达的时间为Y,王明离开家去上学的时间为X,记王明离开家之前能取到牛奶为事件A;
解:设送奶员到达的时间为Y,王明离开家去上学的时间为X,记王明离开家之前能取到牛奶为事件A;
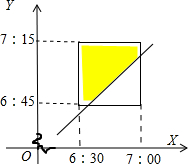
以横坐标表示牛奶送到时间,以纵坐标表示王明离家时间,建立平面直角坐标系,
王明离开家之前不能取到牛奶的事件构成区域如图示:
由于随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.
根据题意,只要点不落到阴影部分,就表示王明离开家之前能取到牛奶,即事件A发生,
所以P(A)=
×
×
=
,
故选:A.
 解:设送奶员到达的时间为Y,王明离开家去上学的时间为X,记王明离开家之前能取到牛奶为事件A;
解:设送奶员到达的时间为Y,王明离开家去上学的时间为X,记王明离开家之前能取到牛奶为事件A;以横坐标表示牛奶送到时间,以纵坐标表示王明离家时间,建立平面直角坐标系,
王明离开家之前不能取到牛奶的事件构成区域如图示:
由于随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.
根据题意,只要点不落到阴影部分,就表示王明离开家之前能取到牛奶,即事件A发生,
所以P(A)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
故选:A.
点评:本题考查几何概型的计算,解题的关键在于设出X、Y,将(X,Y)以及事件A在平面直角坐标系中表示出来.

练习册系列答案
相关题目
若tan(α+β)=3,tan(α-
)=
,则tan(β+
)=( )
| π |
| 4 |
| 4 |
| 3 |
| π |
| 4 |
| A、3 | ||
B、
| ||
C、
| ||
D、-
|
4名男生和2名女生站成一排,则这2名女生不相邻的排法种数( )
| A、600 | B、480 |
| C、360 | D、120 |
在△ABC中,b=2,C=60°,c=
,则角B的大小为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
三个数a,b,c既是等差数列,又是等比数列,则a,b,c间的关系为( )
| A、b-a=c-b | ||||||
| B、b2=ac | ||||||
| C、a=b=c | ||||||
D、
|
设方程tan(x+
)-tan(x-
)=-2的解集为M,方程
-
=-2的解集为N,则( )
| π |
| 4 |
| π |
| 4 |
| 1+tanx |
| 1-tanx |
| tanx-1 |
| tanx+1 |
| A、M=N | B、M?N |
| C、N?M | D、M=Φ |
在△ABC中,若c=acosB,则△ABC中一定为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、锐角三角形 |