题目内容

已知正方形ABCD的边长为1，则|
AB
+
BC
|+|
AB
-
AD
|=（　　）
A、4
B、2
C、
2
D、2
2
考点：向量的加法及其几何意义,向量的减法及其几何意义
专题：平面向量及应用
分析：利用向量的三角形法则和正方形的性质即可得出．
解答： 解：∵正方形ABCD的边长为1，
∴|
AB
+
BC
|+|
AB
-
AD
|=|
AC
|+|
DB
|=2
2
．
故选：D．
点评：本题考查了向量的三角形法则和正方形的性质，属于基础题．
练习册系列答案
相关题目
在2，3，6三个数中随机地抽取一个数记为a，再在剩余的两个数中随机地抽取一个数记为b，则“
a
b
是整数”的概率为
 
．
各项均为正数的等比数列{an}中，a3=a2+8，当a4取最小值时，数列{an}的通项公式an=
 
．
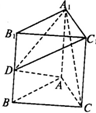如图，直三棱柱ABC-A1B1C1中，AB=AC=1，AA1=2，∠B1A1C1=90°，D为BB1的中点，则异面直线C1D与A1C所成角的余弦值为（　　）
A、
15
15
B、
2
5
7
C、
10
5
D、
10
15
将一个各面都涂了油漆的正方体，切割成1000个同样大小的小正方体．经过搅拌后，从中随机取出一个小正方体，记它的涂油漆面数为X，则X的均值为E（X）=（　　）
A、
27
125
B、
6
5
C、
51
125
D、
3
5
观察下列各式：
2-
2
5
=2
2
5
，
3-
3
10
=3
3
10
，
4-
4
17
=4
4
17
，…．若
9-
m
n
=9
m
n
，则n-m=（　　）
A、43B、57C、73D、91
已知三个球的体积之比为1：8：8，则它们的表面积之比为（　　）
A、1：2：2
B、1：4：8
C、1：4：4
D、1：8：8
若sin（α+β）=
4
5
，sin（α-β）=
3
5
，则
tanα
tanβ
等于（　　）
A、7
B、-7
C、
1
7
D、-
1
7
一个圆柱的母线长度为2，底为半径为1的圆，则此圆柱的侧面积是（　　）
A、πB、2πC、3πD、4π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网