题目内容
14.如图1,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM如图2,设点E是线段DB上的一动点(不与D,B重合).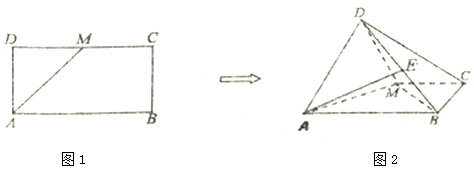
(Ⅰ)当AB=2时,求三棱锥M-BCD的体积;
(Ⅱ)求证:AE不可能与BM垂直.
分析 (Ⅰ)取AM的中点N,连接DN.由已知结合面面垂直的性质可得DN⊥平面ABCM.求出DN,然后利用等积法求得三棱锥M-BCD的体积;
(Ⅱ)假设AE⊥BM,结合(Ⅰ)利用反证法证明.
解答 (Ⅰ)解:取AM的中点N,连接DN.
∵AB=2AD,∴DM=AD,又N为AM的中点,
∴DN⊥AM,
∵平面ADM⊥平面ABCM,又平面ADM∩ABCM=AM,DN?平面ADM,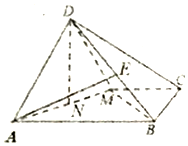
∴DN⊥平面ABCM.
∵AB=2,∴AD=1,AM=$\sqrt{2}$,则$DN=\frac{{\sqrt{2}}}{2}$,
又${S_{△BCM}}=\frac{1}{2}•CM•CB=\frac{1}{2}$,
∴VM-BCD=VD-BCM=$\frac{1}{3}{S}_{△BCM}•DN=\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{12}$;
(Ⅱ)证明:假设AE⊥BM.
由(Ⅰ)可知,DN⊥平面ABCM,∴BM⊥DN.
在长方形ABCD中,AB=2AD,
∴△ADM、△BCM都是等腰直角三角形,∴BM⊥AM.
而DN、AM?平面ADM,DN∩AM=N,
∴BM⊥平面ADM.
而AD?平面ADM,
∴BM⊥AD.
由假设AE⊥BM,AD、AE?平面ABD,AD∩AE=A,
∴BM⊥平面ABD,
而AB?平面ABD,∴BM⊥AB,
这与已知ABCD是长方形矛盾,
故AE不可能与BM垂直.
点评 本题考查直线与平面垂直的性质,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,训练了一种证明几何问题的方法-反证法,属中档题.

练习册系列答案
相关题目
2.已知集合A={x|3≤x<7},B={x|2<x<10},则∁R(A∪B)=( )
| A. | {x|3≤x<7}, | B. | {x|2<x<10} | C. | {x|x≤2或x≥10} | D. | {x|x<3或x≥7} |
9.已知集合A={x∈R||x|≥2},B={x∈R|x2-x-2<0},则下列结论正确的是( )
| A. | A∪B=R | B. | A∩B≠∅ | C. | A∪B=∅ | D. | A∩B=∅ |
3.某理财公司有两种理财产品A和B.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A产品B(其中p、q>0)
(Ⅰ)已知甲、乙两人分别选择了产品A和产品B进行投资,如果一年后他们中至少有一人获利的概率大于$\frac{3}{5}$,求p的取值范围;
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?
产品A产品B(其中p、q>0)
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ |
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?
4.“m≤-$\frac{1}{2}$”是“?x>0,使得$\frac{x}{2}$+$\frac{1}{2x}$-$\frac{3}{2}$>m是真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
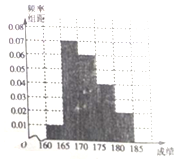 某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示:
某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示: