题目内容
11.若函数f(x)满足$f({x+1})=\frac{1}{f(x)+1}$,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,方程f(x)-4ax-a=0有两个不等的实根,则实数a的取值范围是(-∞,-1)∪(0,$\frac{1}{5}$].分析 求出f(x)在(-1,0)上的解析式,作出函数图形,根据f(x)与直线y=4ax+a有两个交点判断a的临界值,得出a的范围.
解答 解:∵f(x+1)=$\frac{1}{f(x)+1}$,∴f(x)=$\frac{1}{f(x+1)}-1$,
当x∈(-1,0)时,x+1∈(0,1),
∴f(x)=$\frac{1}{x+1}-1$.x∈(-1,0).
作出f(x)在(-1,1]上的函数图形,如图所示:
令f(x)-4ax-a=0得f(x)=4a(x+$\frac{1}{4}$),
∴y=f(x)与直线y=4a(x+$\frac{1}{4}$)在(-1,1]上有两个交点.
若直线y=4a(x+$\frac{1}{4}$)经过点(1,1),则a=$\frac{1}{5}$;
若直线y=4a(x+$\frac{1}{4}$)与y=$\frac{1}{x+1}-1$相切,
联立方程组$\left\{\begin{array}{l}{y=4ax+a}\\{y=\frac{1}{x+1}-1}\end{array}\right.$,消元得4ax2+(5a+1)x+a=0,
令△=(5a+1)2-16a2=0得a=-1或a=-$\frac{1}{9}$.
当a=-$\frac{1}{9}$时,方程的解为x=-$\frac{5a+1}{8a}$=$\frac{1}{2}$,不符合题意;
故a=-1.
∴a<-1或0<a<$\frac{1}{5}$.
故答案为:$({-∞,-1})∪({0,\frac{1}{5}}]$.
点评 本题考查了函数解析式的求解,方程解与函数图形的关系,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
1.已知全集U=R,集合A={x|y=lg(x-1)},B={y|y=$\sqrt{{x}^{2}+2x+5}$},则A∩(∁UB)=( )
| A. | [1,2] | B. | [1,2) | C. | (1,2] | D. | (1,2) |
19.数列{an}满足2nan+1=(n+1)an,其前n项和为Sn,若${a_1}=\frac{1}{2}$,则使得$2-{S_n}<\frac{6}{5}{a_n}$最小的n值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
6.命题“sin2α+cos2α=1恒成立”的否定是( )
| A. | ?α∈R,使得sin2α+cos2α=1 | B. | ?α∈R,使得sin2α+cos2α≠1 | ||
| C. | ?α∈R,使得sin2α+cos2α=1 | D. | ?α∈R,使得sin2α+cos2α≠1 |
16.设a,b都是不等于1的正数,则“${log_a}^2<{log_b}^2$”是“2a>2b>2”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
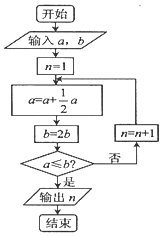 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )