题目内容
3.已知P为圆x2+y2=4上的动点.定点A的坐标为(3,4),则线段AP中点M的轨迹方程(x-$\frac{3}{2}$)2+(y-2)2=1.分析 设M(x,y),利用中点坐标公式得出P点坐标,代入圆的方程化简即可.
解答 解:设M(x,y),则P(2x-3,2y-4),
∵P在圆x2+y2=4上,
∴(2x-3)2+(2y-4)2=4,
化简得:(x-$\frac{3}{2}$)2+(y-2)2=1.
故答案为:(x-$\frac{3}{2}$)2+(y-2)2=1.
点评 本题考查了轨迹方程的求解,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知i为虚数单位,$\overline z$是复数z的共轭复数,若$z=cos\frac{2π}{3}+isin\frac{2π}{3}$,则$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知定义在R上的奇函数f(x),当x≥0时,f(x)单调递增,若不等式f(-4t)>f(2mt2+m)对任意实数t恒成立,则实数m的取值范围是( )
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
15.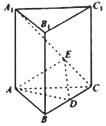 在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
 在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
12.某公共汽车上有10位乘客,沿途5个车站,乘客下车的可能方式有( )种.
| A. | 510 | B. | 105 | C. | 50 | D. | A105 |
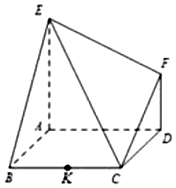 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且$FD=\frac{1}{2}EA=1$.
如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且$FD=\frac{1}{2}EA=1$.