题目内容

18．四面体ABCD四个面重心分别为E、F、G、H，则四面体EFGH表面积与四面体ABCD表面积的比值为1：9．

分析 连接AF、AG并延长与BC、CD相交于M、N，推出四面体EFGH与四面体ABCD是相似的，可求出它们的相似比，面积比是相似比的平方．

解答 解：如图，连接AF、AG并延长与BC、CD相交于M、N，
由于F、G分别是三角形的重心，
所以M、N分别是BC、CD的中点，
且AF：AM=AG：AN=2：3，
所以FG：MN=2：3，
又MN：BD=1：2，所以FG：BD=1：3，
即两个四面体的相似比是1：3，
所以两个四面体的表面积的比是1：9．
故答案为1：9．

点评 本题考查棱锥的结构特征，考查作图能力，是中档题．

练习册系列答案
相关题目
8．下列四个数中最大的是（　　）
A．（ln2）2B．ln（ln2）C．ln$\sqrt{2}$D．ln2
9．△ABC中，角A，B，C所对的边分别为a，b，c，且${a^2}+{b^2}+\sqrt{2}ab={c^2}$，则tanAtan2B的取值范围是$（0，\frac{1}{2}）$．
6．若正数x，y满足$\frac{3}{x}+\frac{1}{y}=1$，则3x+4y的最小值是（　　）
A．24B．28C．30D．25
13．若复数z满足iz=1+3i，则复数z的虚部为（　　）
A．-1B．-iC．1D．i
3．已知函数f（x）=sin2x的图象向右平移$\frac{π}{6}$个单位后，得到函数y=g（x）的图象．下列关于函数y=g（x）的命题：
①g{x}的图象关于点（$\frac{π}{6}$，0）中心对称；
②g（x）的图象关于x=$\frac{π}{6}$轴对称；
③g（x）在区间[$\frac{π}{12}$，$\frac{5π}{12}$]上单调递增．
其中真命题的个数是（　　）
A．0B．1C．2D．3
10．如图，已知$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{BC}$=4$\overrightarrow{BD}$，$\overrightarrow{CA}$=3$\overrightarrow{CE}$，则$\overrightarrow{DE}$=（　　）
A．$\frac{3}{4}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$B．$\frac{5}{12}$$\overrightarrow{b}$-$\frac{3}{4}$$\overrightarrow{a}$C．$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$D．$\frac{5}{12}$$\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$
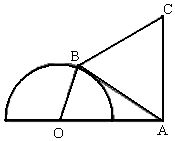7．已知圆C：x2+y2=r2具有如下性质：若M，N是圆C上关于原点对称的两个点，点P是圆C上任意一点，当直线PM，PN的斜率都存在时，记为kPM，kPN，则kPM与kPN之积是一个与点P的位置无关的定值．
利用类比思想，试对椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$写出具有类似特征的性质，并加以证明．
8．如图，半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一点，以AB为一边作等边三角形ABC．当四边形OACB面积最大时，∠AOB=150°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网