题目内容

6．若正数x，y满足$\frac{3}{x}+\frac{1}{y}=1$，则3x+4y的最小值是（　　）
A．24B．28C．30D．25

分析 将3x+4y乘以1，利用已知等式代换，展开，利用基本不等式求最小值．

解答 解：正数x，y满足$\frac{3}{x}+\frac{1}{y}=1$，则（3x+4y）（$\frac{3}{x}+\frac{1}{y}$）=13+$\frac{12y}{x}+\frac{3x}{y}$
≥13+2$\sqrt{\frac{12y}{x}•\frac{3x}{y}}$=25，当且仅当$\frac{12y}{x}=\frac{3x}{y}$时等号成立，所以3x+4y的最小值是25；
故选D．

点评 本题考查了利用基本不等式求最值；关键是1的活用，变形代数式为基本不等式的形式．

练习册系列答案
相关题目
13．已知O是△ABC外接圆的圆心，若4$\overline{OA}$+5$\overrightarrow{OB}$+6$\overline{OC}$=$\overrightarrow{0}$，则cosC=$\frac{\sqrt{7}}{4}$．
17．等比数列{an}的前n项和为Sn，若S14=3S7=3，则S28=（　　）
A．9B．15C．8D．12
14．在平面直角坐标系xOy中，直线l的方程是y=8，圆C的参数方程是$\left\{\begin{array}{l}{x=2+2cosφ}\\{y=2sinφ}\end{array}\right.$（φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求直线l和圆C的极坐标方程；
（2）射线OM：θ=α（其中0＜α＜$\frac{π}{2}$）与圆C交于O，P两点，与直线l交于点M，射线ON：θ=α-$\frac{π}{2}$与圆C交于O，Q两点，与直线l交于点N，求$\frac{|OP|}{|OM|}$•$\frac{|OQ|}{|ON|}$的最大值．
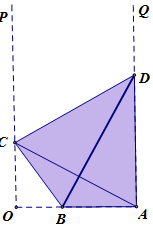1．在国家批复成立江北新区后，南京市政府规划在新区内的一条形地块上新建一个全民健身中心，规划区域为四边形ABCD，如图OP∥AQ，OA⊥AQ，点B在线段OA上，点C、D分别在射线OP与AQ上，且A和C关于BD对称．已知OA=2，
（1）若OC=1，求BD的长；
（2）问点C在何处时，规划区域的面积最小？最小值是多少？
11．已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为2π，最小值为-2，且当x=$\frac{5π}{6}$时，函数取得最大值4．
（I）求函数f（x）的解析式；
（Ⅱ）求函数f（x）的单调递增区间；
（Ⅲ）若当x∈[$\frac{π}{6}$，$\frac{7π}{6}$]时，方程f（x）=m+1有解，求实数m的取值范围．
18．四面体ABCD四个面重心分别为E、F、G、H，则四面体EFGH表面积与四面体ABCD表面积的比值为1：9．
15．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为e=$\frac{1}{2}$，过点（$\sqrt{3}$，$\frac{\sqrt{3}}{2}$）
（I）求椭圆C的方程；
（II）过A（-a，0）且互相垂直的两条直线l1、l2与椭圆C的另一个交点分别为P、Q．问：直线PQ是否经过定点？若是，求出该定点；否则，说明理由．
16．函数y=xsinx+cosx的导数为y′=xcosx．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网