题目内容
10.如图,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{BC}$=4$\overrightarrow{BD}$,$\overrightarrow{CA}$=3$\overrightarrow{CE}$,则$\overrightarrow{DE}$=( )
| A. | $\frac{3}{4}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$ | B. | $\frac{5}{12}$$\overrightarrow{b}$-$\frac{3}{4}$$\overrightarrow{a}$ | C. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | D. | $\frac{5}{12}$$\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$ |
分析 根据向量的三角形法和加减的几何意义即可求出.
解答 解:∵$\overrightarrow{BC}$=4$\overrightarrow{BD}$,
∴$\overrightarrow{DC}$=$\frac{3}{4}$$\overrightarrow{BC}$=$\frac{3}{4}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)
∴$\overrightarrow{DE}$=$\overrightarrow{DC}$+$\overrightarrow{CE}$=$\frac{3}{4}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)+$\frac{1}{3}$$\overrightarrow{CA}$=($\frac{3}{4}$-$\frac{1}{3}$)$\overrightarrow{AC}$-$\frac{3}{4}$$\overrightarrow{AB}$=$\frac{5}{12}$$\overrightarrow{b}$-$\frac{3}{4}$$\overrightarrow{a}$,
故选:B
点评 本题考查了向量的三角形法和向量的数乘运算,属于基础题

练习册系列答案
相关题目
20.执行如图所示的程序框图,如果输入a=6,b=2,则输出的S=( )


| A. | 30 | B. | 120 | C. | 360 | D. | 720 |
5.关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料
试用最小二乘法求出y关于x的线性回归方程
参考公式:
用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
| x | 1 | 2 | 3 | 4 |
| y | 0.5 | 1 | 1.5 | 3 |
参考公式:
用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
2.已知圆的方程为 (x-1)2+(y-1)2=9,P(2,2)是该圆内一点,过点P的最长弦和最短弦分别为AC和BD,则AC•BD=( )
| A. | $6\sqrt{5}$ | B. | $8\sqrt{5}$ | C. | $10\sqrt{5}$ | D. | 2$\sqrt{7}$ |
19.执行如图的程序框图,如果输入的t=0.01,则输出的n=( )


| A. | 5 | B. | 7 | C. | 10 | D. | 12 |
20.若函数f(x)=cos(2x+φ)是奇函数,则φ可取一个值为( )
| A. | -π | B. | -$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
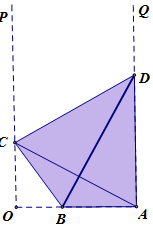 在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图OP∥AQ,OA⊥AQ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知OA=2,
在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图OP∥AQ,OA⊥AQ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知OA=2,