题目内容
8.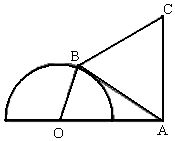 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.当四边形OACB面积最大时,∠AOB=150°.
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.当四边形OACB面积最大时,∠AOB=150°.
分析 设∠AOB=θ,并根据余弦定理,表示出△ABC的面积及△OAB的面积,进而表示出四边形OACB的面积,并化简函数的解析式为正弦型函数的形式,再结合正弦型函数最值的求法进行求解.
解答 解:四边形OACB的面积=△OAB的面积+△ABC的面积,设∠AOB=θ,
则△ABC的面积=$\frac{1}{2}$•AB•AC•sin60°=$\frac{\sqrt{3}}{4}$•AB2=$\frac{\sqrt{3}}{4}$(OA2+OB2-2OA•OB•sinθ)=$\frac{\sqrt{3}}{4}$(5-4cosθ),
△OAB的面积=$\frac{1}{2}$•OA•OB•sinθ=$\frac{1}{2}•2•1•sinθ$=sinθ,
四边形OACB的面积=$\frac{\sqrt{3}}{4}$(5-4cosθ)+sinθ=$\frac{5\sqrt{3}}{4}$-$\sqrt{3}$cosθ+sinθ=$\frac{5\sqrt{3}}{4}$+2sin(θ-60°),
故当θ-60°=90°,即θ=150°时,四边形OACB的面积最大值为$\frac{5\sqrt{3}}{4}$+2,
故答案为:150°.
点评 函数y=Asin(ωx+φ)(A>0,ω>0)中,最大值或最小值由A确定,即要求三角函数的周期与最值一般是要将其函数的解析式化为正弦型函数,再根据最大值为|A|、最小值为-|A|求解,属于中档题.

练习册系列答案
相关题目
19.执行如图的程序框图,如果输入的t=0.01,则输出的n=( )


| A. | 5 | B. | 7 | C. | 10 | D. | 12 |
3.已知$\overrightarrow{a}$=(1,0),|$\overrightarrow{b}$|=$\sqrt{2}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
20.若函数f(x)=cos(2x+φ)是奇函数,则φ可取一个值为( )
| A. | -π | B. | -$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
17.已知数列{an}是等差数列,a1+a3=2,a3+a5=4,则a5+a7=( )
| A. | 6 | B. | 8 | C. | 12 | D. | 16 |