题目内容
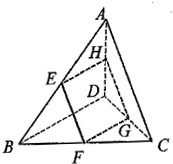 如图E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
如图E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.(1)求证:四边形EFGH为平行四边形.
(2)若AC与BD满足什么条件时,四边形EFGH为菱形,试证明你的结论.
(3)求证:AC∥平面EFGH.
考点:直线与平面平行的判定,棱锥的结构特征
专题:空间位置关系与距离
分析:(1)连接BD,利用三角形中位线定理推导出EH∥FG,且EH=FG,由此能证明四边形EFGH为平行四边形.
(2)AC=BD时,四边形EFGH为菱形.由(1)知四边形EFGH为平行四边形,且FG=
BD,由E、F分别是AB、BC的中点,知EF=
AC,由AC=BD,得EF=FG,由此证明四边形EFGH为菱形.
(3)E、F分别是AB、BC的中点,得EF∥AC,由此能证明AC∥平面EFGH.
(2)AC=BD时,四边形EFGH为菱形.由(1)知四边形EFGH为平行四边形,且FG=
| 1 |
| 2 |
| 1 |
| 2 |
(3)E、F分别是AB、BC的中点,得EF∥AC,由此能证明AC∥平面EFGH.
解答:
(1)证明:连接BD,因为EH是△ABD的中位线,
所以EH∥BD,且FG=
BD,
同理,FG∥BD,且FG=
BD,
因为EH∥FG,且EH=FG,
所以,四边形EFGH为平行四边形.
(2)解:AC=BD时,四边形EFGH为菱形.
证明:由(1)知四边形EFGH为平行四边形,且FG=
BD,
∵E、F分别是AB、BC的中点,
∴EF=
AC,∵AC=BD,∴EF=FG,
∴四边形EFGH为菱形.
(3)证明:∵E、F分别是AB、BC的中点,
∴EF∥AC,
∵AC不色含于平面EFGH,EF?平面EFGH,
∴AC∥平面EFGH.
所以EH∥BD,且FG=
| 1 |
| 2 |
同理,FG∥BD,且FG=
| 1 |
| 2 |
因为EH∥FG,且EH=FG,
所以,四边形EFGH为平行四边形.
(2)解:AC=BD时,四边形EFGH为菱形.
证明:由(1)知四边形EFGH为平行四边形,且FG=
| 1 |
| 2 |
∵E、F分别是AB、BC的中点,
∴EF=
| 1 |
| 2 |
∴四边形EFGH为菱形.
(3)证明:∵E、F分别是AB、BC的中点,
∴EF∥AC,
∵AC不色含于平面EFGH,EF?平面EFGH,
∴AC∥平面EFGH.
点评:本题考查四边形是平行四边形的证明,考查四边形为菱形所满足条件的判断与证明,考查直线与平面平行的证明,解题时要认真审题,注意三角形中位线定理的灵活运用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目

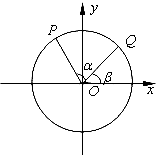 如图,以x轴负半轴为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(-
如图,以x轴负半轴为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(- 如图,MA⊥平面ABCD,四边形ABCD为菱形,四边形ADNM为平行四边形,点E为AB中点.
如图,MA⊥平面ABCD,四边形ABCD为菱形,四边形ADNM为平行四边形,点E为AB中点. 如图,在三棱锥S-ABC中,SC⊥平面ABC,M、N分别是SB和SC的中点,设MN=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°
如图,在三棱锥S-ABC中,SC⊥平面ABC,M、N分别是SB和SC的中点,设MN=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60° 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB= 如图,AP是⊙O的切线,A为切点,AE=3,EC=4,BE=6,PE=6,则AP=
如图,AP是⊙O的切线,A为切点,AE=3,EC=4,BE=6,PE=6,则AP= 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,