题目内容
 如图,在三棱锥S-ABC中,SC⊥平面ABC,M、N分别是SB和SC的中点,设MN=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°
如图,在三棱锥S-ABC中,SC⊥平面ABC,M、N分别是SB和SC的中点,设MN=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°(Ⅰ)求证:平面AMN⊥平面SAC;
(Ⅱ)求二面角M-AB-C的平面角的余弦值;
(Ⅲ)求AN和CM所成角的余弦值.
考点:异面直线及其所成的角,平面与平面垂直的判定,与二面角有关的立体几何综合题
专题:空间角
分析:(I)根据线面垂直的性质可得SC⊥BC,结合∠ACB=90°及线面垂直的判定定理可得BC⊥平面SAC,由三角形中位线定理可得MN∥BC,结合线面垂直的第二判定定理可得MN⊥平面SAC,最后由面面垂直的判定定理得到平面AMN⊥平面SAC.
(Ⅱ)取BC的中点D,连MD,在平面ABC内作DE⊥AB于E,连ME,可证得∠MED即为二面角M-AB-C的平面角,解三角形MED可得二面角M-AB-C的平面角的正切值;
(Ⅲ)作作AF
CD,则AF
MN,可证得∠CMF或其补角即为AN与CM所成的角,解三角形CMF可得AN和CM所成角的余弦值.
(Ⅱ)取BC的中点D,连MD,在平面ABC内作DE⊥AB于E,连ME,可证得∠MED即为二面角M-AB-C的平面角,解三角形MED可得二面角M-AB-C的平面角的正切值;
(Ⅲ)作作AF
| ∥ |
. |
| ∥ |
. |
解答:
(Ⅰ)证明:∵SC⊥平面ABC,∴SC⊥BC,
又∵∠ACB=90°∴AC⊥BC,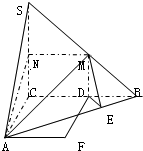
∵AC∩SC=C,BC⊥平面SAC,又∵M,N是SC、SB的中点
∴MN∥BC,∴MN⊥面SAC,
∵MN?平面AMN,∴面AMNAMN⊥面SAC.
(Ⅱ)解:取BC的中点D,连MD,
在平面ABC内作DE⊥AB于E,连ME,
由M,D分别为SB,BC的中点,
可得MD∥SC,MD=
SC
由SC⊥平面ABC,可得MD⊥平面ABC,
则∠MED即为二面角M-AB-C的平面角,
∵直线AM与直线SC所成的角60°,MD∥SC,
∴∠AMD=60°,
∵MN=AC=CD=BD=1,
∴AD=
,MD=
,DE=
,ME=
,
∴cos∠MED=
=
=
.
(Ⅲ)解:作AF
CD,则AF
MN,
即四边形AFMN为平行四边形,
则AN∥FM,
则∠CMF或其补角即为AN与CM所成的角,
∵CM=MF=
,CF=
,
由余弦定理得cos∠CMF=
,
∴AN和CM所成角的余弦值为
.
又∵∠ACB=90°∴AC⊥BC,

∵AC∩SC=C,BC⊥平面SAC,又∵M,N是SC、SB的中点
∴MN∥BC,∴MN⊥面SAC,
∵MN?平面AMN,∴面AMNAMN⊥面SAC.
(Ⅱ)解:取BC的中点D,连MD,
在平面ABC内作DE⊥AB于E,连ME,
由M,D分别为SB,BC的中点,
可得MD∥SC,MD=
| 1 |
| 2 |
由SC⊥平面ABC,可得MD⊥平面ABC,
则∠MED即为二面角M-AB-C的平面角,
∵直线AM与直线SC所成的角60°,MD∥SC,
∴∠AMD=60°,
∵MN=AC=CD=BD=1,
∴AD=
| 2 |
| ||
| 3 |
| ||
| 5 |
| ||
| 15 |
∴cos∠MED=
| DE |
| ME |
| ||||
|
| ||
| 13 |
(Ⅲ)解:作AF
| ∥ |
. |
| ∥ |
. |
即四边形AFMN为平行四边形,
则AN∥FM,
则∠CMF或其补角即为AN与CM所成的角,
∵CM=MF=
| ||
| 3 |
| 2 |
由余弦定理得cos∠CMF=
| 2 |
| 5 |
∴AN和CM所成角的余弦值为
| 2 |
| 5 |
点评:本题考查的知识点是平面与平面垂直的判定,异面直线及其所成的角,二面角的平面角及求法,其中构造出空间线面夹角,异面直线夹角的平面角,将空间角问题转化为解三角形问题是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.
如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.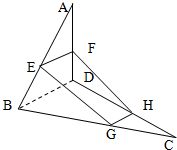 如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且
如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且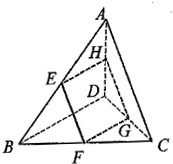 如图E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
如图E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.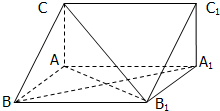 直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=
直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=