题目内容
 如图,MA⊥平面ABCD,四边形ABCD为菱形,四边形ADNM为平行四边形,点E为AB中点.
如图,MA⊥平面ABCD,四边形ABCD为菱形,四边形ADNM为平行四边形,点E为AB中点.(Ⅰ)求证:AN∥平面MEC;
(Ⅱ)求证:AC⊥平面BDN.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(I)由已知条件推导出四边形MNCB是平行四边形,平行四边形MNCB对角线MC、NB相交且互相平分,设其交点为F,则NF=FB,连接EF,由三角形中位定理能证明AN∥平面MEC.
( II) 连接BD,由线面垂直得MA⊥AC,由MA∥ND,得ND⊥AC,由菱形性质得BD⊥AC,由此能证明AC⊥平面BDN.
( II) 连接BD,由线面垂直得MA⊥AC,由MA∥ND,得ND⊥AC,由菱形性质得BD⊥AC,由此能证明AC⊥平面BDN.
解答:
证明:(I)∵四边形ABCD是菱形,四边形ADNM是平行四边形
∴MN∥AD∥BC且MN=AD=BC,
∴四边形MNCB也是平行四边形,…(2分)
∴平行四边形MNCB对角线MC、NB相交且互相平分,设其交点为F,
∴NF=FB,连接EF
在△ABN中,EF为中位线,即EF∥AN,…(4分)
又AN平包含于平面MEC,EF?平面MEC,…(5分)
∴AN∥平面MEC.…(6分)
( II) 连接BD,∵MA⊥平面ABCD且AC?平面ABCD,
∴MA⊥AC,…(7分)
又MA∥ND,∴ND⊥AC,…(9分)
又四边形ABCD是菱形,∴BD⊥AC,…(10分)
又ND和BD是平面BDN上的两相交直线,…(11分)
∴AC⊥平面BDN.…(12分)
∴MN∥AD∥BC且MN=AD=BC,
∴四边形MNCB也是平行四边形,…(2分)
∴平行四边形MNCB对角线MC、NB相交且互相平分,设其交点为F,
∴NF=FB,连接EF
在△ABN中,EF为中位线,即EF∥AN,…(4分)
又AN平包含于平面MEC,EF?平面MEC,…(5分)
∴AN∥平面MEC.…(6分)
( II) 连接BD,∵MA⊥平面ABCD且AC?平面ABCD,
∴MA⊥AC,…(7分)
又MA∥ND,∴ND⊥AC,…(9分)
又四边形ABCD是菱形,∴BD⊥AC,…(10分)
又ND和BD是平面BDN上的两相交直线,…(11分)
∴AC⊥平面BDN.…(12分)
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.
如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.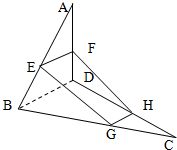 如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且
如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且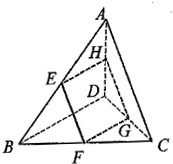 如图E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
如图E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点. 如图所示,正方体ABCD-A1B1C1D1中,侧面对角线AB1,BC1上分别有一点E,F,且B1E=C1F,则直线EF与平面ABCD的位置关系是
如图所示,正方体ABCD-A1B1C1D1中,侧面对角线AB1,BC1上分别有一点E,F,且B1E=C1F,则直线EF与平面ABCD的位置关系是